题目内容
一个空间几何体G-ABCD的三视图如图所示,其中Ai,Bi,Ci,Di,Gi(i=1,2,3)分别是A,B,C,D,G在直立、侧立、水平三个投影面内的投影.在视图中,四边形A1B2C3D4为正方形,且A1B2=2a;在侧视图中,A2D2⊥A2G2;在俯视图中,G3D3=G3C3=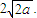
(Ⅰ)根据三视图画出几何体的直观图,并标明A,B,C,D,G五点的位置;
(Ⅱ)证明:平面AGD⊥平面BGC;
(Ⅲ)求三棱锥D-ACG的体积.
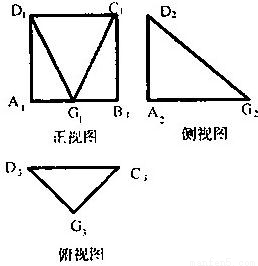
【答案】分析:(1)由三视图我们可以判断这个几何体是四棱锥,又由四边形A1B2C3D4为正方形,且A1B2=2a;在侧视图中,A2D2⊥A2G2;在俯视图中,G3D3=G3C3=.我们易画出几何体的直观图.
(2)由(1)的直观图我们易判断AG⊥平面BCG,根据面面垂直的判断定理,我们易得到平面AGD⊥平面BGC;
(3)利用转化思想,三棱锥D-ACG的体积可转化为三棱锥G-ACD的体积,根据(1)中分析出的棱长关系,我们易代入求出三棱锥D-ACG的体积.
解答: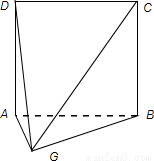 解:(Ⅰ)空间几何体的直观图如图所示,
解:(Ⅰ)空间几何体的直观图如图所示,
且可得到平面ABCD⊥平面ABG,四边形
ABCD为正方形,AG=BG=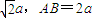 ,
,
故AG⊥BG(4分)
(Ⅱ)∵平面ABCD⊥平面ABG,
面ABCD∩平面ABG=AB,CB⊥AB,
∴CB⊥平面ABG,故CB⊥AG(6分)
又AG⊥BG,∴AG⊥平面BGC.
∴平面AGD⊥平面BGC(8分)
(Ⅲ)过G作GE⊥AB,垂足为E,
则GE⊥平面ABCD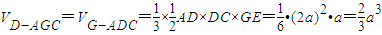 .(12分)
.(12分)
点评:本题考查的知识点是由三视图求体积,根据三视图分析出几何体的形状及相关棱的长度和棱的关系是解答本题的关键.
(2)由(1)的直观图我们易判断AG⊥平面BCG,根据面面垂直的判断定理,我们易得到平面AGD⊥平面BGC;
(3)利用转化思想,三棱锥D-ACG的体积可转化为三棱锥G-ACD的体积,根据(1)中分析出的棱长关系,我们易代入求出三棱锥D-ACG的体积.
解答:
 解:(Ⅰ)空间几何体的直观图如图所示,
解:(Ⅰ)空间几何体的直观图如图所示,且可得到平面ABCD⊥平面ABG,四边形
ABCD为正方形,AG=BG=
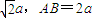 ,
,故AG⊥BG(4分)
(Ⅱ)∵平面ABCD⊥平面ABG,
面ABCD∩平面ABG=AB,CB⊥AB,
∴CB⊥平面ABG,故CB⊥AG(6分)
又AG⊥BG,∴AG⊥平面BGC.
∴平面AGD⊥平面BGC(8分)
(Ⅲ)过G作GE⊥AB,垂足为E,
则GE⊥平面ABCD
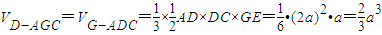 .(12分)
.(12分)点评:本题考查的知识点是由三视图求体积,根据三视图分析出几何体的形状及相关棱的长度和棱的关系是解答本题的关键.

练习册系列答案
相关题目
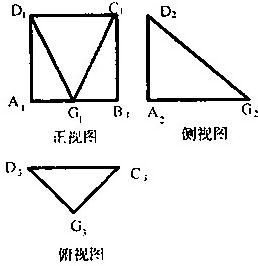 一个空间几何体G-ABCD的三视图如图所示,其中Ai,Bi,Ci,Di,Gi(i=1,2,3)分别是A,B,C,D,G在直立、侧立、水平三个投影面内的投影.在视图中,四边形A1B2C3D4为正方形,且A1B2=2a;在侧视图中,A2D2⊥A2G2;在俯视图中,G3D3=G3C3=
一个空间几何体G-ABCD的三视图如图所示,其中Ai,Bi,Ci,Di,Gi(i=1,2,3)分别是A,B,C,D,G在直立、侧立、水平三个投影面内的投影.在视图中,四边形A1B2C3D4为正方形,且A1B2=2a;在侧视图中,A2D2⊥A2G2;在俯视图中,G3D3=G3C3=