题目内容
设A是由n个有序实数构成的一个数组,记作:A=(a1,a2,…,ai,…,an).其中ai(i=1,2,…,n)称为数组A的“元”,S称为A的下标.如果数组S中的每个“元”都是来自 数组A中不同下标的“元”,则称A=(a1,a2,…,an)为B=(b1,b2,…bn)的子数组.定义两个数组A=(a1,a2,…,an),B=(b1,b2,…,bn)的关系数为C(A,B)=a1b1+a2b2+…+anbn.(Ⅰ)若
 ,B=(-1,1,2,3),设S是B的含有两个“元”的子数组,求C(A,S)的最大值;
,B=(-1,1,2,3),设S是B的含有两个“元”的子数组,求C(A,S)的最大值;(Ⅱ)若
 ,B=(0,a,b,c),且a2+b2+c2=1,S为B的含有三个“元”的子数组,求C(A,S)的最大值;
,B=(0,a,b,c),且a2+b2+c2=1,S为B的含有三个“元”的子数组,求C(A,S)的最大值;(Ⅲ)若数组A=(a1,a2,a3)中的“元”满足
 .设数组Bm(m=1,2,3,…,n)含有四个“元”bm1,bm2,bm3,bm4,且
.设数组Bm(m=1,2,3,…,n)含有四个“元”bm1,bm2,bm3,bm4,且 ,求A与Bm的所有含有三个“元”的子数组的关系数C(A,Bm)(m=1,2,3,…,n)的最大值.
,求A与Bm的所有含有三个“元”的子数组的关系数C(A,Bm)(m=1,2,3,…,n)的最大值.
【答案】分析:(Ⅰ)依据题意中“元”的含义,可知当S=(-1,3)时,C(A,S)取得最大值为2.
(Ⅱ)对0是不是S中的“元”进行分类讨论:①当0是S中的“元”时,由于A的三个“元”都相等,及B中a,b,c三个“元”的对称性,利用平均值不等式计算C(A,S)=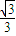 (a+b)的最大值,②当0不是S中的“元”时,只须计算C(A,S)=
(a+b)的最大值,②当0不是S中的“元”时,只须计算C(A,S)=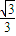 (a+b+c)的最大值即可,最后综上即可得出C(A,S)的最大值.
(a+b+c)的最大值即可,最后综上即可得出C(A,S)的最大值.
(Ⅲ)由于Bm=(bm1,bm2,bm3,bm4)满足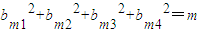 .及bm1,bm2,bm3,bm4关系的对称性,只需考虑(bm2,bm3,bm4)与(a1,a2,a3)的关系数的情况.下面分情况讨论:当bm1=0时,当
.及bm1,bm2,bm3,bm4关系的对称性,只需考虑(bm2,bm3,bm4)与(a1,a2,a3)的关系数的情况.下面分情况讨论:当bm1=0时,当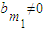 时,得出a1bm2+a2bm3+a3bm4的最大值的情况.最后综合得出C(A,Bm)的最大值即可.
时,得出a1bm2+a2bm3+a3bm4的最大值的情况.最后综合得出C(A,Bm)的最大值即可.
解答:解:(Ⅰ)依据题意,当S=(-1,3)时,C(A,S)取得最大值为2.
(Ⅱ)①当0是S中的“元”时,由于A的三个“元”都相等及B中a,b,c三个“元”的对称性,可以只计算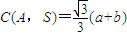 的最大值,其中a2+b2+c2=1.
的最大值,其中a2+b2+c2=1.
由(a+b)2=a2+b2+2ab≤2(a2+b2)≤2(a2+b2+c2)=2,
得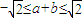 .
.
当且仅当c=0,且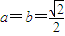 时,a+b达到最大值
时,a+b达到最大值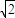 ,
,
于是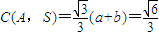 .
.
②当0不是S中的“元”时,计算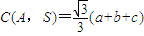 的最大值,
的最大值,
由于a2+b2+c2=1,
所以(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.≤3(a2+b2+c2)=3,
当且仅当a=b=c时,等号成立.
即当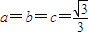 时,a+b+c取得最大值
时,a+b+c取得最大值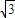 ,此时
,此时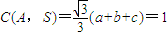 .
.
综上所述,C(A,S)的最大值为1.
(Ⅲ)因为Bm=(bm1,bm2,bm3,bm4)满足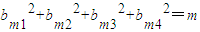 .
.
由bm1,bm2,bm3,bm4关系的对称性,只需考虑(bm2,bm3,bm4)与(a1,a2,a3)的关系数的情况.
当bm1=0时,有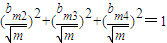 .
.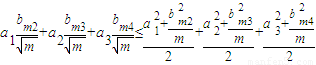 =
=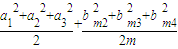 =
=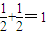 .
.
即bm1=0,且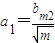 ,
,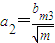 ,
,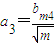 时,a1bm2+a2bm3+a3bm4的最大值为
时,a1bm2+a2bm3+a3bm4的最大值为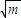 .
.
当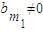 时,
时,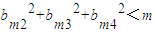 ,
,
得a1bm2+a2bm3+a3bm4最大值小于 .
.
所以C(A,Bm)的最大值为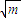 (m=1,2,3,…,n).
(m=1,2,3,…,n).
点评:本小题主要考查函数与方程的综合运用、平均值不等式在函数极值中的应用等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.
(Ⅱ)对0是不是S中的“元”进行分类讨论:①当0是S中的“元”时,由于A的三个“元”都相等,及B中a,b,c三个“元”的对称性,利用平均值不等式计算C(A,S)=
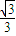 (a+b)的最大值,②当0不是S中的“元”时,只须计算C(A,S)=
(a+b)的最大值,②当0不是S中的“元”时,只须计算C(A,S)=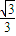 (a+b+c)的最大值即可,最后综上即可得出C(A,S)的最大值.
(a+b+c)的最大值即可,最后综上即可得出C(A,S)的最大值.(Ⅲ)由于Bm=(bm1,bm2,bm3,bm4)满足
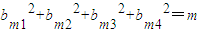 .及bm1,bm2,bm3,bm4关系的对称性,只需考虑(bm2,bm3,bm4)与(a1,a2,a3)的关系数的情况.下面分情况讨论:当bm1=0时,当
.及bm1,bm2,bm3,bm4关系的对称性,只需考虑(bm2,bm3,bm4)与(a1,a2,a3)的关系数的情况.下面分情况讨论:当bm1=0时,当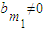 时,得出a1bm2+a2bm3+a3bm4的最大值的情况.最后综合得出C(A,Bm)的最大值即可.
时,得出a1bm2+a2bm3+a3bm4的最大值的情况.最后综合得出C(A,Bm)的最大值即可.解答:解:(Ⅰ)依据题意,当S=(-1,3)时,C(A,S)取得最大值为2.
(Ⅱ)①当0是S中的“元”时,由于A的三个“元”都相等及B中a,b,c三个“元”的对称性,可以只计算
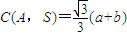 的最大值,其中a2+b2+c2=1.
的最大值,其中a2+b2+c2=1.由(a+b)2=a2+b2+2ab≤2(a2+b2)≤2(a2+b2+c2)=2,
得
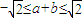 .
.当且仅当c=0,且
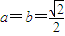 时,a+b达到最大值
时,a+b达到最大值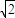 ,
,于是
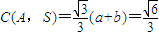 .
.②当0不是S中的“元”时,计算
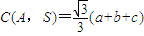 的最大值,
的最大值,由于a2+b2+c2=1,
所以(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.≤3(a2+b2+c2)=3,
当且仅当a=b=c时,等号成立.
即当
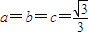 时,a+b+c取得最大值
时,a+b+c取得最大值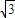 ,此时
,此时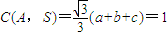 .
.综上所述,C(A,S)的最大值为1.
(Ⅲ)因为Bm=(bm1,bm2,bm3,bm4)满足
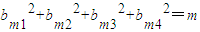 .
.由bm1,bm2,bm3,bm4关系的对称性,只需考虑(bm2,bm3,bm4)与(a1,a2,a3)的关系数的情况.
当bm1=0时,有
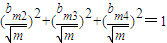 .
.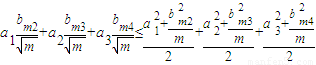 =
=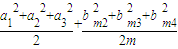 =
=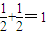 .
.即bm1=0,且
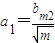 ,
,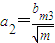 ,
,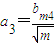 时,a1bm2+a2bm3+a3bm4的最大值为
时,a1bm2+a2bm3+a3bm4的最大值为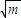 .
.当
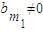 时,
时,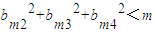 ,
,得a1bm2+a2bm3+a3bm4最大值小于
 .
.所以C(A,Bm)的最大值为
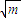 (m=1,2,3,…,n).
(m=1,2,3,…,n).点评:本小题主要考查函数与方程的综合运用、平均值不等式在函数极值中的应用等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目
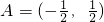 ,B=(-1,1,2,3),设S是B的含有两个“元”的子数组,求C(A,S)的最大值;
,B=(-1,1,2,3),设S是B的含有两个“元”的子数组,求C(A,S)的最大值;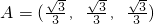 ,B=(0,a,b,c),且a2+b2+c2=1,S为B的含有三个“元”的子数组,求C(A,S)的最大值.
,B=(0,a,b,c),且a2+b2+c2=1,S为B的含有三个“元”的子数组,求C(A,S)的最大值. ,B=(-1,1,2,3),设S是B的含有两个“元”的子数组,求C(A,S)的最大值;
,B=(-1,1,2,3),设S是B的含有两个“元”的子数组,求C(A,S)的最大值; ,B=(0,a,b,c),且a2+b2+c2=1,S为B的含有三个“元”的子数组,求C(A,S)的最大值.
,B=(0,a,b,c),且a2+b2+c2=1,S为B的含有三个“元”的子数组,求C(A,S)的最大值.