题目内容
△ABC的面积为S,三边长为a、b、c.(1)求证:(a+b+c)2<4(ab+bc+ca)
(2)若S=(a+b)2-c2,a+b=4,求S的最大值.
(3)试比较a2+b2+c2与
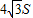 的大小.
的大小.
【答案】分析:(1)直接两边作差,把平方展开,整理后结合三角形三边关系即可得到结论;
(2)直接根据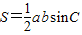 ,c2=a2+b2-2abcosC以及S=(a+b)2-c2,a+b=4,代入整理得到sinC=4cosC+4求出sinC;再结合基本不等式求出ab的取值范围即可得到结论;
,c2=a2+b2-2abcosC以及S=(a+b)2-c2,a+b=4,代入整理得到sinC=4cosC+4求出sinC;再结合基本不等式求出ab的取值范围即可得到结论;
(3)通过作差结合三角形的面积公式以及余弦定理整理得到=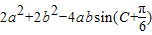 ≥2(a-b)2≥0即可得到结论.
≥2(a-b)2≥0即可得到结论.
解答:解:(1)证明:∵(a+b+c)2-4(ab+bc+ca)=a2+b2+c2-2ab-2ac-2bc=(a2-ab-ac)+(b2-ab-bc)+(c2-ac-bc)=a(a-b-c)+b(b-a-c)+c(c-a-b)
∵a、b、c为△ABC的三边
∴b+c>a a+c>b a+b>c
故(a+b+c)2<4(ab+bc+ca)(4分)
(2)∵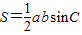 ,c2=a2+b2-2abcosC
,c2=a2+b2-2abcosC
∴
把a+b=4代入整理得:
∴sinC=4cosC+4⇒17cos2C+32cosC+15=0⇒cosC=-1或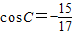
∵C∈(0,π)∴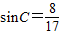 (8分)
(8分)
∴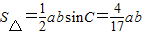
而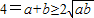 ∴ab∈(0,4]
∴ab∈(0,4]
∴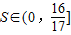 (10分)
(10分)
(3)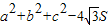
=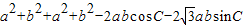
=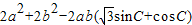
=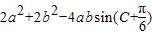 ≥2(a-b)2≥0
≥2(a-b)2≥0
∴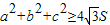 (14分)
(14分)
点评:本题综合考查不等式的证明以及三角形中的几何计算.考查计算能力与分析问题的能力.通常不等式的证明采用作差法.
(2)直接根据
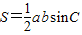 ,c2=a2+b2-2abcosC以及S=(a+b)2-c2,a+b=4,代入整理得到sinC=4cosC+4求出sinC;再结合基本不等式求出ab的取值范围即可得到结论;
,c2=a2+b2-2abcosC以及S=(a+b)2-c2,a+b=4,代入整理得到sinC=4cosC+4求出sinC;再结合基本不等式求出ab的取值范围即可得到结论;(3)通过作差结合三角形的面积公式以及余弦定理整理得到=
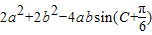 ≥2(a-b)2≥0即可得到结论.
≥2(a-b)2≥0即可得到结论.解答:解:(1)证明:∵(a+b+c)2-4(ab+bc+ca)=a2+b2+c2-2ab-2ac-2bc=(a2-ab-ac)+(b2-ab-bc)+(c2-ac-bc)=a(a-b-c)+b(b-a-c)+c(c-a-b)
∵a、b、c为△ABC的三边
∴b+c>a a+c>b a+b>c
故(a+b+c)2<4(ab+bc+ca)(4分)
(2)∵
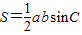 ,c2=a2+b2-2abcosC
,c2=a2+b2-2abcosC∴

把a+b=4代入整理得:
∴sinC=4cosC+4⇒17cos2C+32cosC+15=0⇒cosC=-1或
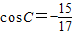
∵C∈(0,π)∴
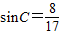 (8分)
(8分)∴
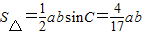
而
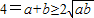 ∴ab∈(0,4]
∴ab∈(0,4]∴
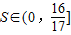 (10分)
(10分)(3)
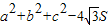
=
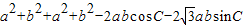
=
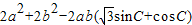
=
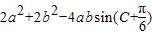 ≥2(a-b)2≥0
≥2(a-b)2≥0∴
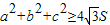 (14分)
(14分)点评:本题综合考查不等式的证明以及三角形中的几何计算.考查计算能力与分析问题的能力.通常不等式的证明采用作差法.

练习册系列答案
相关题目