题目内容
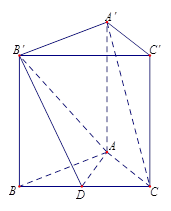
如图,四棱锥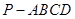 中,侧面
中,侧面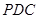 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是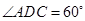 的菱形,
的菱形,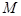 为
为 的中点.
的中点.

(Ⅰ)求 与底面
与底面 所成角的大小;
所成角的大小;
(Ⅱ)求证: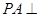 平面
平面 ;(Ⅲ)求二面角
;(Ⅲ)求二面角 的余弦值.
的余弦值.
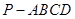 中,侧面
中,侧面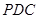 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是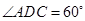 的菱形,
的菱形,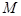 为
为 的中点.
的中点.
(Ⅰ)求
 与底面
与底面 所成角的大小;
所成角的大小;(Ⅱ)求证:
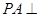 平面
平面 ;(Ⅲ)求二面角
;(Ⅲ)求二面角 的余弦值.
的余弦值. (Ⅰ) 45°; (Ⅱ)参考解析; (Ⅲ) -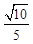
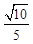
试题分析:(Ⅰ) 由于平面PDC垂直于平面AC,并且三角形PDC是等边三角形.所以通过做DC边上的高PO.即可得直线
 与底面
与底面 所成角为∠PAO.通过底面AC是菱形可求得AO,所以通过解直角三角形PAO即可求得∠PAO 的大小.即为结论.
所成角为∠PAO.通过底面AC是菱形可求得AO,所以通过解直角三角形PAO即可求得∠PAO 的大小.即为结论.(Ⅱ) 通过建立空间坐标系,写出相关点A,P,D,B,C,M的坐标.计算出向量PA,向量DM,向量DC.通过向量PA与向量DM的数量积为0可得这两条直线垂直.同理可以证明PA垂直于DC.从而可得直线PA垂直于平面CDM.即通过向量知识证得线面垂直.
(Ⅲ)求二面角
 的余弦值通过求出平面DCM和平面BCM的法向量.再求两法向量的夹角的余弦值的绝对值,再根据图形判断正负即可.
的余弦值通过求出平面DCM和平面BCM的法向量.再求两法向量的夹角的余弦值的绝对值,再根据图形判断正负即可.试题解析:(I)取DC的中点O,由ΔPDC是正三角形,有PO⊥DC.
又∵平面PDC⊥底面ABCD,∴PO⊥平面ABCD于O.连结OA,则OA是PA在底面上的射影.
∴∠PAO就是PA与底面所成角.∵∠ADC=60°,由已知ΔPCD和ΔACD是全等的正三角形,从而求得OA=OP=
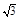 .∴∠PAO=45°.∴PA与底面ABCD可成角的大小为45°.
.∴∠PAO=45°.∴PA与底面ABCD可成角的大小为45°.(II)由底面ABCD为菱形且∠ADC=60°,DC=2,DO=1,有OA⊥DC.建立空间直角坐标系如图,则
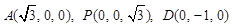 ,
, 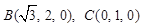 .
.由M为PB中点,
∴
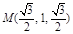 .∴
.∴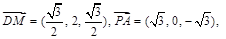
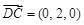 .∴
.∴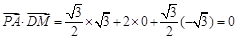 ,
,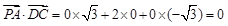 .
.∴PA⊥DM,PA⊥DC. ∴PA⊥平面DMC.
(III)
 .令平面BMC的法向量
.令平面BMC的法向量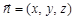 ,
,则
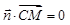 ,从而x+z=0; ……①,
,从而x+z=0; ……①, 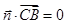 ,从而
,从而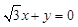 . ……②
. ……②由①、②,取x=?1,则
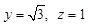 . ∴可取
. ∴可取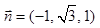 .
.由(II)知平面CDM的法向量可取
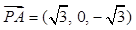 ,
, ∴
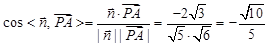 .∴所求二面角的余弦值为-
.∴所求二面角的余弦值为-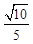 .…13分
.…13分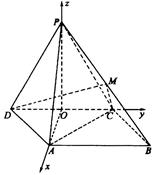

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
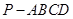 中,底面
中,底面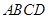 是矩形,四条侧棱长均相等且
是矩形,四条侧棱长均相等且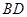 交
交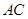 于点
于点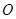 .
.
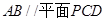 ;
;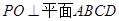 .
.

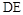
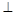 平面
平面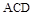 ,
,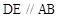 ,
,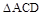 是正三角形,AD=DE
是正三角形,AD=DE AB,且F是CD的中点.
AB,且F是CD的中点.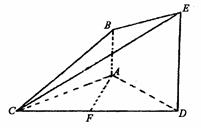
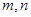 与平面
与平面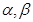 ,有下列四个命题:
,有下列四个命题: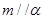 ,
,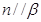 ,且
,且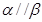 ,则
,则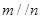 ;
;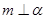 ,
,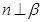 ,且
,且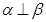 ,则
,则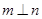 ;
;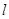 和平面
和平面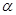 ,若
,若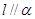 ,
,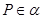 ,过点
,过点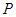 且平行于
且平行于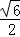
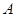 、
、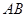 为正方体的两个顶点,
为正方体的两个顶点,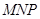 、
、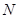 、
、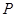 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出