题目内容
已知实数4,m,9构成一个等比数列,则圆锥曲线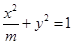 的离心率为( )
的离心率为( )
A.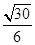 | B.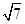 | C.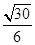 或 或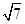 | D.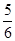 或 或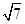 |
C
解析试题分析:因为已知实数4,m,9构成一个等比数列,所以可得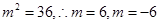 .所以圆锥曲线为椭圆时即
.所以圆锥曲线为椭圆时即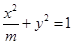 的方程为
的方程为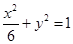 .所以
.所以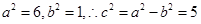 .所以离心率
.所以离心率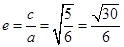 .当是双曲线时可求得离心率为
.当是双曲线时可求得离心率为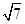 .故选C.
.故选C.
考点:1.数列的思想.2.圆锥曲线的性质.3.离心率的计算.4.分类的思想.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
过抛物线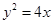 焦点
焦点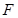 的直线交其于
的直线交其于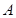 ,
,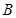 两点,
两点,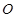 为坐标原点.若
为坐标原点.若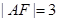 ,则
,则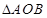 的面积为( )
的面积为( )
A.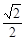 | B.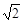 | C.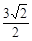 | D.2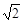 |
双曲线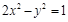 的离心率为( )
的离心率为( )
A.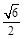 | B.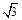 | C.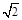 | D. |
已知抛物线x2=4y上有一条长为6的动弦AB,则AB中点到x轴的最短距离为( )
A. | B. | C.1 | D.2 |
已知M是y= x2上一点,F为抛物线的焦点.A在C:(x-1)2+(y-4)2=1上,则|MA|+|MF|的最小值为( )
x2上一点,F为抛物线的焦点.A在C:(x-1)2+(y-4)2=1上,则|MA|+|MF|的最小值为( )
| A.2 | B.4 | C.8 | D.10 |
已知双曲线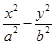 =1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
=1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
| A.|OA|>|OB| | B.|OA|<|OB| |
| C.|OA|=|OB| | D.|OA|与|OB|大小关系不确定 |
已知椭圆C: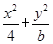 =1,直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
=1,直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
| A.[1,4) | B.[1,+∞) | C.[1,4)∪(4,+∞) | D.(4,+∞) |
以抛物线y2=8x上的任意一点为圆心作圆与直线x+2=0相切,这些圆必过一定点,则这一定点的坐标是( )
| A.(0,2) | B.(2,0) |
| C.(4,0) | D.(0,4) |
设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5.若以MF为直径的圆过点(0,2),则C的方程为( )
| A.y2=4x或y2=8x | B.y2=2x或y2=8x |
| C.y2=4x或y2=16x | D.y2=2x或y2=16x |