题目内容
在四棱锥 中,
中,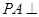 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形, ,
, .
.
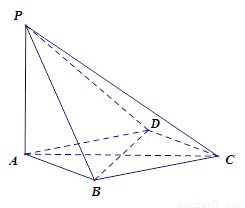
(1)求证: 平面PAC;
平面PAC;
(2)若 ,求PB与AC所成角的余弦值;
,求PB与AC所成角的余弦值;
(3)若PA= ,求证:平面PBC⊥平面PDC
,求证:平面PBC⊥平面PDC
【答案】
(1)由线线平行证得 (2)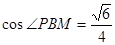 (3)求得
(3)求得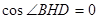 从而证明.
从而证明.
【解析】
试题分析:(1)证:因为四边形ABCD是菱形,
所以AC⊥BD.又因为PA⊥平面ABCD. 所以PA⊥BD,又AC∩PA=A
所以BD⊥平面PAC.
(2)解:过B作BM//AC交DA延长线于M,连接PM ∠PBM或其补角为所求
因为BM//AC
AM//BC 所以四边形MACB为平行四边形 所以BM=AC=2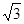 ,PB=PM=
,PB=PM= ,所以
,所以
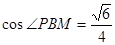 .
.
(3) 作BH⊥PC,连接HD
 PA⊥平面ABCD,AD="AB"
PA⊥平面ABCD,AD="AB" 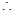 PB=PD,又
PB=PD,又 CD="CB"
PC="PC"
CD="CB"
PC="PC"  △PBC≌△PDC
△PBC≌△PDC
 BH⊥PC
BH⊥PC
 HD⊥PC 因此∠BHD为二面角B-PC-D的平面角
HD⊥PC 因此∠BHD为二面角B-PC-D的平面角
因为AP=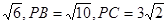 BC="2" 有BH=
BC="2" 有BH=
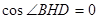 所以
面PBC⊥面PDC.
所以
面PBC⊥面PDC.
考点:直线与平面垂直的判定;点、线、面间的距离计算;用空间向量求直线间的夹角、距离.
点评:本小题主要考查空间线面关系的垂直关系的判断、异面直线所成的角、用空间向量的方法求解直线的
夹角、距离等问题,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算
求解能力.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
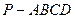 中,平面PAD⊥平面ABCD,
中,平面PAD⊥平面ABCD,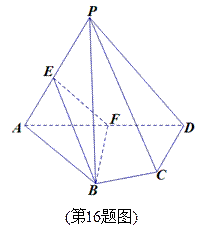
 中,
中, 平面
平面 ,底面
,底面 .
. 时,求证:
时,求证: ;
; 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.


 ,
, ………………2分
………………2分 ,得证。
,得证。 ,只要
,只要
 ,即
,即 ………6分
………6分
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以

 ………………3分
………………3分
 中,
中,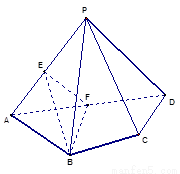
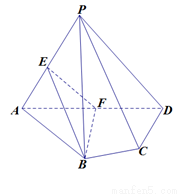
 中,平面PAD⊥平面ABCD, AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面ABCD, AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点