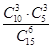题目内容
一圆形餐桌依次有A、B、C、D、E、F共有6个座位.现让3个大人和3 个小孩入座进餐,要求任何两个小孩都不能坐在一起,则不同的入座方法总 数为( )
| A.6 | B.12 | C.144 | D.72 |
D
解析从题意:将一圆形餐桌依次有A、B、C、D、E、F共有6个座位、看成一排,任何两个小孩都不能坐在一起,那么大人也不能坐在一起.看作两种类型:一是大、小、大、小、大、小;二是小、大、小、大、小、大.
解:一圆形餐桌依次有A、B、C、D、E、F共有6个座位、不妨看作是大、小、大、小、大、小或者
小、大、小、大、小、大两类型,三个大人的入座方法A33种,三个小孩的入座方法A33种,因而不同的入座方法总数为2A33?A33=72.
故选D

练习册系列答案
相关题目
从5位男教师和4位女教师中选出3位教师,派到3个班担任班主任(每班1位
班主任),要求这3位班主任中男、女教师都要有,则不同的选派方案共有 ( )
| A.210种 | B.420种 | C.630种 | D.840种 |
.从不同号码的 双鞋中任取
双鞋中任取 只,其中恰好有
只,其中恰好有 双的取法种数为( )
双的取法种数为( )
A. | B. | C. | D.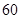 |
若 ,则
,则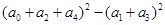 的值为( )
的值为( )
A. | B. | C. | D. |
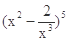 展开式中的常数项为 .(用数字作答)
展开式中的常数项为 .(用数字作答) ,有
,有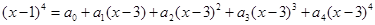 ,
,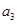 的值为 .
的值为 .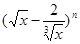 展开式中所有项的二项式系数和为32,则其展开式中的常数项为 .
展开式中所有项的二项式系数和为32,则其展开式中的常数项为 .