题目内容
设函数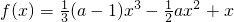 (a∈R)[
(a∈R)[
(Ⅰ)若y=f(x)在点(1,f(1))处的切线与y轴和直线x-2y=0围成的三角形面积等于 ,求a的值;
,求a的值;
(II)当a<2时,讨论f(x)的单调性.
解:(I)∵f'(x)=(a-1)x2-ax+1,∴f'(1)=(a-1)+1-a=0
又∵f(1)= (a-1)-
(a-1)- a+1=-
a+1=- ,
,
∴y=f(x)在点(1,f(1))处的切线的方程为y=- ,
,
由 ,得
,得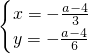 ,
,
则切线与y轴和直线x-2y=0围成的三角形面积等于 ×
×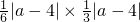 =
= ,
,
解得,a=7或a=1.
(II)f'(x)=(a-1)x2-ax+1=(x-1)[(a-1)x-1]
①当a=1时,f′(x)=1-x,则f(x)在(-∞,1]上是增函数,在[1,+∞)上是减函数;
②当1<a<2时,f′(x)≤0得1≤a≤ ,则f(x)在(-∞,1]、[
,则f(x)在(-∞,1]、[ ,+∞)上是增函数,在[1,
,+∞)上是增函数,在[1, ]上是减函数;
]上是减函数;
③当a<1时,f′(x)≥0得 ≤a≤1,则f(x)在(-∞,
≤a≤1,则f(x)在(-∞, ],[1,+∞)上是减函数,在[
],[1,+∞)上是减函数,在[ ,1]上是增函数.
,1]上是增函数.
分析:(I)由题目条件知,点P(1,f(1))为切点,且函数在该点处的导数值为切线的斜率,求出切线方程,利用切线与y轴和直线x-2y=0围成的三角形面积,从而建立关于a的方程,可求得a的值;
(II)由函数及其导数的解析式,解不等式f'(x)>0与f'(x)<0,可求出函数的单调区间.
点评:本题主要考查了利用导数研究函数的单调性,同时考查了导数的几何意义,以及学生灵活转化题目条件的能力,属于中档题.
又∵f(1)=
 (a-1)-
(a-1)- a+1=-
a+1=- ,
,∴y=f(x)在点(1,f(1))处的切线的方程为y=-
 ,
,由
 ,得
,得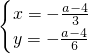 ,
,则切线与y轴和直线x-2y=0围成的三角形面积等于
 ×
×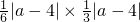 =
= ,
,解得,a=7或a=1.
(II)f'(x)=(a-1)x2-ax+1=(x-1)[(a-1)x-1]
①当a=1时,f′(x)=1-x,则f(x)在(-∞,1]上是增函数,在[1,+∞)上是减函数;
②当1<a<2时,f′(x)≤0得1≤a≤
 ,则f(x)在(-∞,1]、[
,则f(x)在(-∞,1]、[ ,+∞)上是增函数,在[1,
,+∞)上是增函数,在[1, ]上是减函数;
]上是减函数;③当a<1时,f′(x)≥0得
 ≤a≤1,则f(x)在(-∞,
≤a≤1,则f(x)在(-∞, ],[1,+∞)上是减函数,在[
],[1,+∞)上是减函数,在[ ,1]上是增函数.
,1]上是增函数.分析:(I)由题目条件知,点P(1,f(1))为切点,且函数在该点处的导数值为切线的斜率,求出切线方程,利用切线与y轴和直线x-2y=0围成的三角形面积,从而建立关于a的方程,可求得a的值;
(II)由函数及其导数的解析式,解不等式f'(x)>0与f'(x)<0,可求出函数的单调区间.
点评:本题主要考查了利用导数研究函数的单调性,同时考查了导数的几何意义,以及学生灵活转化题目条件的能力,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
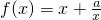 (a∈R),函数g(x)的图象与函数f(x)的图象关于点A(1,2)对称.
(a∈R),函数g(x)的图象与函数f(x)的图象关于点A(1,2)对称. (a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x,y)使得f(f(y))=y,则a的取值范围是( )
(a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x,y)使得f(f(y))=y,则a的取值范围是( ) (a∈R),函数g(x)的图象与函数f(x)的图象关于点A(1,2)对称.
(a∈R),函数g(x)的图象与函数f(x)的图象关于点A(1,2)对称. (a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x0,y0)使得f(f(y0))=y0,则a的取值范围是( )
(a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x0,y0)使得f(f(y0))=y0,则a的取值范围是( ) (a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是( )
(a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是( )