题目内容
今有标号为1,2,3,4,5的五封信,另有同样标号的五个信封.现将五封信任意地装入五个信封,每个信封装入一封信,试求至少有两封信配对的概率.
解:设恰有两封信配对为事件A,
恰有三封信配对为事件B,
恰有四封信(也即五封信配对)为事件C,
则“至少有两封信配对”事件等于A+B+C,且A、B、C两两互斥.
∵P(A)= ,P(B)=
,P(B)= ,P(C)=
,P(C)=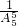 ,
,
∴所求概率P(A)+P(B)+P(C)= .
.
答:至少有两封信配对的概率是 .
.
分析:至少有两封信配对包括恰有两封信配对、恰有三封信配对、恰有五封信配对三种情况,而这三种情况对应事件为互斥事件,故分别求概率再取和即可.而每种情况对应的概率可由古典概型求解.
点评:本题考查古典概型、互斥事件的概率加法、排列、组合等知识,考查分析问题、解决问题的能力.
恰有三封信配对为事件B,
恰有四封信(也即五封信配对)为事件C,
则“至少有两封信配对”事件等于A+B+C,且A、B、C两两互斥.
∵P(A)=
 ,P(B)=
,P(B)= ,P(C)=
,P(C)=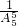 ,
,∴所求概率P(A)+P(B)+P(C)=
 .
.答:至少有两封信配对的概率是
 .
.分析:至少有两封信配对包括恰有两封信配对、恰有三封信配对、恰有五封信配对三种情况,而这三种情况对应事件为互斥事件,故分别求概率再取和即可.而每种情况对应的概率可由古典概型求解.
点评:本题考查古典概型、互斥事件的概率加法、排列、组合等知识,考查分析问题、解决问题的能力.

练习册系列答案
相关题目