题目内容
一个长方体的对角线长为l，全面积为S，给出下列四个实数对：①（8，128）；②（7，50）；③（6，80）；④（
，
），其中可作为（l，S）取值的实数对的序号是 ．
【答案】分析：本题考查的是长方体的对角线和侧面积问题．在解答时，要充分考虑长方体体所满足的几何特征，从而转化出必备条件结合条件即可获得问题的解答．具体解答时可以先设出相邻三棱长进而找到对角线与侧面积之间的关系．
解答：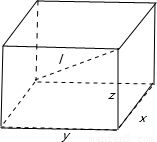
解：由题意可知：如图
设长方体的相邻三棱长分别为x、y、z．
则：l2=x2+y2+z2
S=2（xy+xz+yz）=2xy+2xz+2yz
又∵S=2xy+2xz+2yz≤（x2+y2）+（x2+z2）+（y2+z2）
=2（x2+y2+z2）=2•l2，
当且仅当x=y=z时等号成立．
由S≤2•l2又因为：
128≤2×64=128成立、50＜2×49=98成立、80＜2×36=72不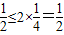成立、
成立．
故答案为：①②④．
点评：本题考查的是长方体的对角线和侧面积问题．在解答的过程当中充分体现了数据的处理转化、图形的观察利用以及基本不等式的利用．值得同学们体会反思．
解答：
解：由题意可知：如图设长方体的相邻三棱长分别为x、y、z．
则：l2=x2+y2+z2
S=2（xy+xz+yz）=2xy+2xz+2yz
又∵S=2xy+2xz+2yz≤（x2+y2）+（x2+z2）+（y2+z2）
=2（x2+y2+z2）=2•l2，
当且仅当x=y=z时等号成立．
由S≤2•l2又因为：
128≤2×64=128成立、50＜2×49=98成立、80＜2×36=72不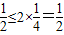成立、
成立．故答案为：①②④．
点评：本题考查的是长方体的对角线和侧面积问题．在解答的过程当中充分体现了数据的处理转化、图形的观察利用以及基本不等式的利用．值得同学们体会反思．
练习册系列答案
相关题目
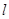，全面积为S，给出下列四个实数对：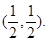
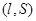取值的实数对的序号是 ▲
。
，