题目内容
某学校高一年级开设了A，B，C，D，E五门选修课．为了培养学生的兴趣爱好，要求每个学生必须参加且只能选修一门课程．假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的．（Ⅰ）求甲、乙、丙三名学生参加五门选修课的所有选法种数；
（Ⅱ）求甲、乙、丙三名学生中至少有两名学生选修同一门课程的概率；
（Ⅲ）设随机变量X为甲、乙、丙这三名学生参加A课程的人数，求X的分布列与数学期望．
分析：（Ⅰ）每个学生选修一门课程，有5种选法，由分步乘法原理即可求解．
（Ⅱ）“甲、乙、丙三名学生中至少有两名学生选修同一门课程”的对立事件为“三名学生选择三门不同选修课程”，利用对立事件的概率关系求解．
（Ⅲ）X的所有可能取值为：0，1，2，3，利用古典概型分别求概率，列出分布列求期望即可．
（Ⅱ）“甲、乙、丙三名学生中至少有两名学生选修同一门课程”的对立事件为“三名学生选择三门不同选修课程”，利用对立事件的概率关系求解．
（Ⅲ）X的所有可能取值为：0，1，2，3，利用古典概型分别求概率，列出分布列求期望即可．
解答：解：（Ⅰ）甲、乙、丙三名学生每人选择五门选修课的方法数是5种，
故共有5×5×5=125（种）．
（Ⅱ）三名学生选择三门不同选修课程的概率为：
=
．
∴三名学生中至少有两人选修同一门课程的概率为：1-
=
．
（Ⅲ）由题意：X=0，1，2，3
.P(X=0)=
=
；
P(X=1)=
=
；
P(X=2)=
=
；
P(X=3)=
=
．
ξ的分布列为
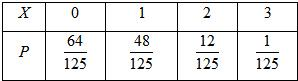
数学期望EX=0×
+1×
+2×
+3×
=
．
故共有5×5×5=125（种）．
（Ⅱ）三名学生选择三门不同选修课程的概率为：
| ||
| 53 |
| 12 |
| 25 |
∴三名学生中至少有两人选修同一门课程的概率为：1-
| 12 |
| 25 |
| 13 |
| 25 |
（Ⅲ）由题意：X=0，1，2，3
.P(X=0)=
| 43 |
| 53 |
| 64 |
| 125 |
P(X=1)=
| ||
| 53 |
| 48 |
| 125 |
P(X=2)=
| ||
| 53 |
| 12 |
| 125 |
P(X=3)=
| ||
| 53 |
| 1 |
| 125 |
ξ的分布列为
数学期望EX=0×
| 64 |
| 125 |
| 48 |
| 125 |
| 12 |
| 125 |
| 1 |
| 125 |
| 3 |
| 5 |
点评：本题考查计数原理、古典概型、及离散型随机变量的分布列和期望，难度不大．
练习册系列答案
相关题目
本小题共13分）
五门选修课．为了培养学生的兴趣爱好，要求每个学生必须参加且只能选修
一门课程．假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的．
为甲、乙、丙这三名学生参加
课程的人数，求
五门选修课．为了培养学生的兴趣爱好，要求每个学生必须参加且只能选修一门课程．假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的．
为甲、乙、丙这三名学生参加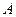
课程的人数，求