题目内容
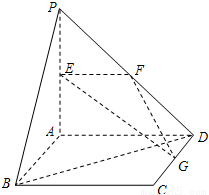
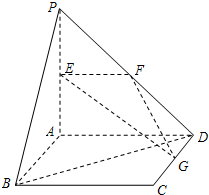如图，直线PA⊥平面ABCD，四边形ABCD是正方形，且PA=AD=2，点E、F、G分别是线段PA、PD、CD的中点．
（1）求四棱锥B-ADFE的体积；
（2）求异面直线EG与AD所成角的大小（结果用反三角表示）．
解：（1）AB为四棱锥的高等于2，所以 SADFE=
=
，
VB-ADFE=
SADFE•AB=1．
（2）取AB的中点H，则HG∥AD，所以，∠HGE即为异面直线EG与AD所成角．
AG=
，EG=
，HG=2，EH=
．
所以，Rt△EHG中，tan∠EGH=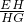
=
．
即异面直线EF与AG所成角为arctan．
分析：（1）AB为四棱锥的高等于2，利用梯形的面积公式求出 SADFE，代入四棱锥B-ADFE的体积公式VB-ADFE=SADFE•AB，运算求得结果．
（2）取AB的中点H，则∠HGE即为异面直线EG与AD所成角，Rt△EHG中，由tan∠EGH=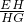的值 求出∠EGH 的大小．
点评：本题主要考查求棱锥的体积，异面直线所成的角的定义和求法，找出两异面直线所成的角，是解题的关键．
=，VB-ADFE=
SADFE•AB=1．（2）取AB的中点H，则HG∥AD，所以，∠HGE即为异面直线EG与AD所成角．
AG=
，EG=，HG=2，EH=．所以，Rt△EHG中，tan∠EGH=
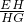=．即异面直线EF与AG所成角为arctan
．分析：（1）AB为四棱锥的高等于2，利用梯形的面积公式求出 SADFE，代入四棱锥B-ADFE的体积公式VB-ADFE=
SADFE•AB，运算求得结果．（2）取AB的中点H，则∠HGE即为异面直线EG与AD所成角，Rt△EHG中，由tan∠EGH=
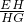的值 求出∠EGH 的大小．点评：本题主要考查求棱锥的体积，异面直线所成的角的定义和求法，找出两异面直线所成的角，是解题的关键．
练习册系列答案
口算小状元口算速算天天练系列答案
天天练口算系列答案
相关题目
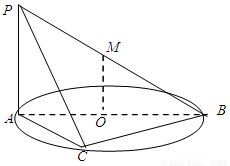
10、如图，直线PA垂直于圆O所在的平面，△ABC内接于圆O，且AB为圆O的直径，点M为线段PB的中点．现有以下命题：①BC⊥PC；②OM∥平面APC；③点B到平面PAC的距离等于线段BC的长．其中真命题的个数为（ ）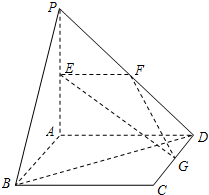
（2011•崇明县二模）如图，直线PA⊥平面ABCD，四边形ABCD是正方形，且PA=AD=2，点E、F、G分别是线段PA、PD、CD的中点．
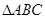内接于圆O，且AB为圆O的直径，点M为线段PB的中点．现有以下命题：①
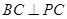；②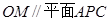
；③点A到平面PBC距离就是△PAC的PC边上的高．④二面角P-BC-A大小不可能为450，其中真命题的个数为 （ ）
