题目内容
在对人们的休闲方式的一次调查中,共调查了 人,其中女性
人,其中女性 人,男性
人,男性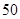 人.女性中有
人.女性中有 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有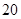 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动.
人主要的休闲方式是运动.
(1)根据以上数据建立一个 的列联表;
的列联表;
(2)判断性别与休闲方式是否有关系.
【答案】
(1)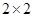 的列联表:
的列联表:
|
性别 休闲方式 |
看电视 |
运动 |
总计 |
|
女 |
45 |
25 |
70 |
|
男 |
20 |
30 |
50 |
|
总计 |
65 |
55 |
120 |
(2)有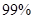 的把握认为“休闲方式与性别有关”。
的把握认为“休闲方式与性别有关”。
【解析】
试题分析:(1)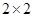 的列联表:
的列联表:
|
性别 休闲方式 |
看电视 |
运动 |
总计 |
|
女 |
45 |
25 |
70 |
|
男 |
20 |
30 |
50 |
|
总计 |
65 |
55 |
120 |
6分
(2)假设“休闲方式与性别无关”
计算
因为 ,而
,而 ,
,
所以有理由认为假设“休闲方式与性别无关”是不合理的。
即有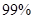 的把握认为“休闲方式与性别有关”。……12分
的把握认为“休闲方式与性别有关”。……12分
考点:本题主要考查列联表,独立性假设检验。
点评:中档题,此类问题解法明确,关键是理解题意,应用公式准确计算。卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,卡方值越大,越不符合,偏差越小,卡方值就越小,越趋于符合,若量值完全相等时,卡方值就为0,表明理论值完全符合。

练习册系列答案
相关题目
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)能否在犯错误的概率不超过0.025的前提下认为性别与休闲方式有关系.
参考公式及临界值表如下:k2=
(1)根据以上数据建立一个2×2的列联表;
(2)能否在犯错误的概率不超过0.025的前提下认为性别与休闲方式有关系.
参考公式及临界值表如下:k2=

| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)能否在犯错误的概率不超过0.025的前提下认为性别与休闲方式有关系.
参考公式及临界值表如下:k2=
(1)根据以上数据建立一个2×2的列联表;
(2)能否在犯错误的概率不超过0.025的前提下认为性别与休闲方式有关系.
参考公式及临界值表如下:k2=

| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

 人,其中女性
人,其中女性 人,男性
人,男性 人.女性中有
人.女性中有 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动.
人主要的休闲方式是运动. 的列联表;
的列联表;