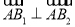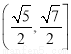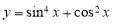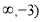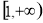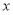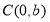题目内容
已知函数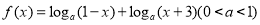
(1)求函数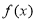 的定义域;
的定义域;
(2)求函数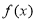 的零点;
的零点;
(3)若函数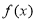 的最小值为-4,求a的值.
的最小值为-4,求a的值.
(1)函数的定义域为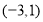 ;(2
;(2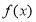 的零点是
的零点是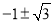 ;(3)
;(3)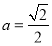 .
.
【解析】
试题分析:(1)函数的定义域是使函数有意义的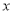 取值范围,而对数有意义则真数大于0,即
取值范围,而对数有意义则真数大于0,即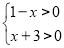 ;
;
(2)函数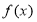 的零点等价于方程
的零点等价于方程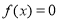 的根,可先利用对数运算性质
的根,可先利用对数运算性质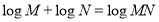 进行化简,即
进行化简,即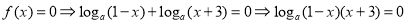
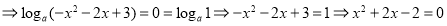 ,要注意定义域的范围,检验解得的根是否在定义域内;
,要注意定义域的范围,检验解得的根是否在定义域内;
(3)可利用函数的单调性求最值来解参数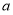 ,由(2)可知
,由(2)可知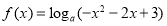 ,令
,令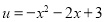 ,
,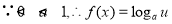 在
在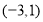 单调递减,则
单调递减,则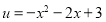 在
在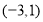 取最大值时函数
取最大值时函数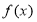 的最小值取-4,而
的最小值取-4,而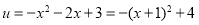 ,当
,当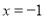 时
时 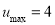 ,则
,则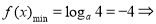
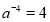 ,
,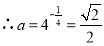 .
.
试题解析:21.( 普通班)
(1)要使函数有意义,则有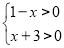 解之得
解之得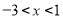 ,
,
所以函数的定义域为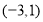 .
.
(2)函数可化为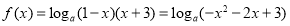
由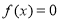 ,得
,得 , 即
, 即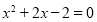 ,
,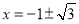 ,
,
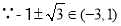 ,
,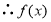 的零点是
的零点是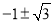 .
.
21.(联办班)
(1)要使函数有意义:则有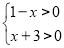 ,解之得:
,解之得: 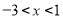 ,
,
所以函数的定义域为: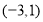 .
.
(2)函数可化为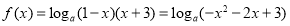
由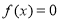 ,得
,得 ,即
,即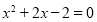 ,
,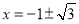 ,
,
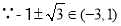 ,
,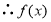 的零点是
的零点是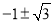 .
.
(3)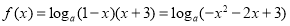
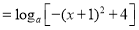
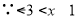
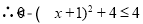 .
.
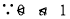 ,
,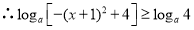 ,
,
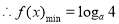 .由
.由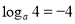 ,得
,得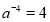 ,
,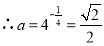 .
.
考点:1、对数函数的定义域;2对数的运算性质;3、函数的零点;4、对数方程的解法;5、复合函数的最值问题;6、二次函数的最值.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目