题目内容
下列说法:①方程2-x+x2=3的实数解的个数为1;
②函数y=ax的图象可以由函数y=2ax(其中a>0且a≠1)平移得到;
③若对x∈R,有f(x-1)=-f(x),则f(x)的周期为2;
④函数y=f(1+x)与函数y=f(1-x)的图象关于直线x=1对称.
其中正确的命题的序号 .
【答案】分析:利用函数图象的交点个数,来判断方程的解的个数,从而判断①是否正确;
根据函数图象的变化规律判断②是否正确;
利用周期函数的定义,验证③是否正确;
根据函数图象上的任一点关于直线的对称点是否在另一函数图象上,来判断两函数图象是否关于直线对称,从而判断④是否正确.
解答: 解:对①选项,利用函数f(x)=2-x=
解:对①选项,利用函数f(x)=2-x= 与f(x)=3-x2的图象,判断两函数的图象有两个交点,∴方程有两个实数解,故①错误;
与f(x)=3-x2的图象,判断两函数的图象有两个交点,∴方程有两个实数解,故①错误;
对②选项,函数y=ax的图象可由函数y=2ax的图象的点,横坐标不变,纵坐标缩短为原来的 得到,∴②错误;
得到,∴②错误;
对③选项,∵f(x)=-f(x-1),∴f(x+2)=-f(x+1)=-[-f(x)]=f(x).∴则f(x)的周期为2,故③正确;
对④选项,对函数y=f(1+x)图象上任一点P(a,b),关于x=1的对称点Q(2-a,b),∵f(2-a)=f[1+(1-a)]=f[1-(1-a)]=f(a)=b,
∴Q在函数y=f(1-x)的图象上,故④正确.
故答案是③④.
点评:本题借助考查判断的真假判定,考查函数零点的判定、函数的图象变化规律及函数的周期.
根据函数图象的变化规律判断②是否正确;
利用周期函数的定义,验证③是否正确;
根据函数图象上的任一点关于直线的对称点是否在另一函数图象上,来判断两函数图象是否关于直线对称,从而判断④是否正确.
解答:
 解:对①选项,利用函数f(x)=2-x=
解:对①选项,利用函数f(x)=2-x= 与f(x)=3-x2的图象,判断两函数的图象有两个交点,∴方程有两个实数解,故①错误;
与f(x)=3-x2的图象,判断两函数的图象有两个交点,∴方程有两个实数解,故①错误;对②选项,函数y=ax的图象可由函数y=2ax的图象的点,横坐标不变,纵坐标缩短为原来的
 得到,∴②错误;
得到,∴②错误;对③选项,∵f(x)=-f(x-1),∴f(x+2)=-f(x+1)=-[-f(x)]=f(x).∴则f(x)的周期为2,故③正确;
对④选项,对函数y=f(1+x)图象上任一点P(a,b),关于x=1的对称点Q(2-a,b),∵f(2-a)=f[1+(1-a)]=f[1-(1-a)]=f(a)=b,
∴Q在函数y=f(1-x)的图象上,故④正确.
故答案是③④.
点评:本题借助考查判断的真假判定,考查函数零点的判定、函数的图象变化规律及函数的周期.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的实数解的个数为1;
的实数解的个数为1;
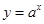 的图象可以由函数
的图象可以由函数 (其中
(其中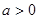 且
且 )平移得到;
)平移得到;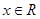 ,有
,有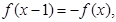 则
则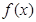 的周期为2;
的周期为2; 与函数
与函数 的图象关于直线
的图象关于直线 对称.
对称.