题目内容
已知服从正态分布N( ,
, )的随机变量在区间(
)的随机变量在区间( ,
, ),(
),( ,
, ),和(
),和( ,
, )内取值的概率分别为68.3%,95.4%,和99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高(单位:cm)服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制( )
)内取值的概率分别为68.3%,95.4%,和99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高(单位:cm)服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制( )
| A.683套 | B.954套 | C.972套 | D.997套 |
B
解析试题分析:由于,服从正态分布N( ,
, )的随机变量在区间(
)的随机变量在区间( ,
, ),(
),( ,
, ),和(
),和( ,
, )内取值的概率分别为68.3%,95.4%,和99.7%.所以,当学生的身高(单位:cm)服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制套数为1000×95.4%=954,,故选B。
)内取值的概率分别为68.3%,95.4%,和99.7%.所以,当学生的身高(单位:cm)服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制套数为1000×95.4%=954,,故选B。
考点:正态分布
点评:简单题,根据随机变量在区间( ,
, )内取值的概率为95.4%,确定定制套数。
)内取值的概率为95.4%,确定定制套数。

练习册系列答案
相关题目
抛掷一枚质地均匀的骰子,落地后记事件A为“奇数点向上”,事件B为“偶数点向上”,事件C为“向上的点数是2的倍数”,事件D为“2点或4点向上”。则下列每对事件是互斥但不对立的是( )
| A.A与B | B.B与C | C.C与D | D.A与D |
若 ,则
,则 的值使得过
的值使得过 可以做两条直线与圆
可以做两条直线与圆
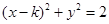 相切的概率等于( )
相切的概率等于( )
A. | B. | C. | D.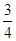 |
在区间[-1,1]上随机取一个数 ,则
,则 的值介于
的值介于 与
与 之间的概率为( )
之间的概率为( )
A. | B. | C. | D. |
从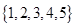 中随机选取一个数
中随机选取一个数 ,从
,从 中随机选取一个数
中随机选取一个数 ,则
,则 的概率是( )
的概率是( )
A. | B. | C. | D. |
某产品分甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.03,丙级品的概率为0.01,则对成品抽查一件抽得正品的概率为( )
| A.0.99 | B.0.98 | C.0.97 | D.0.96 |





 ,则事件A在一次试验中出现的概率是
,则事件A在一次试验中出现的概率是