题目内容
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆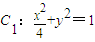 .
.(1)若椭圆
 ,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由;
,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由;(2)写出与椭圆C1相似且短半轴长为b的椭圆Cb的方程;若在椭圆Cb上存在两点M、N关于直线y=x+1对称,求实数b的取值范围?
(3)如图:直线y=x与两个“相似椭圆”
 和
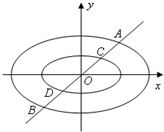
和 分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
【答案】分析:(1)分别求出特征三角形是腰长为a 和底边长为2c,从而得到椭圆的相似比.
(2)设出椭圆Cb的方程,直线lMN的方程,根据两点关于直线对称的性质,求出直线lMN的方程,根据直线lMN与椭圆Cb有两个不同的交点,判别式大于零,求得实数b的取值范围.
(3)作法:过原点作直线y=kx(k≠1),交椭圆M和椭圆Mλ于点E和点F,则△CDF和△ABE即为所求相似三角形,且相似比为λ.
解答:解:(1)椭圆C2与C1相似. 因为椭圆C2的特征三角形是腰长为a=4,底边长为2c=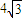 的等腰三角形,
的等腰三角形,
而椭圆C1的特征三角形是腰长为2,底边长为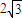 的等腰三角形,因此两个等腰三角形相似,且相似比为2.
的等腰三角形,因此两个等腰三角形相似,且相似比为2.
(2)椭圆Cb的方程为: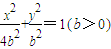 ,
,
设lMN:y=-x+t,点M(x1,y1),N(x2,y2),MN中点为(x,y),
则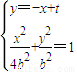 ,所以5x2-8tx+4(t2-b2)=0,则
,所以5x2-8tx+4(t2-b2)=0,则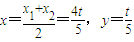 .
.
因为中点在直线y=x+1上,所以有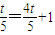 ,
,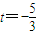 ,即直线lMN的方程为:
,即直线lMN的方程为: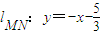 ,
,
由题意可知,直线lMN与椭圆Cb有两个不同的交点,
即方程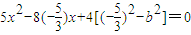 有两个不同的实数解,
有两个不同的实数解,
所以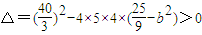 ,即
,即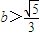 .
.
(3)作法:过原点作直线y=kx(k≠1),交椭圆M和椭圆Mλ于点E和点F,则△CDF和△ABE即为所求相似三角形,且相似比为λ.
点评:本题考查直线和圆锥曲线的位置关系,两点关于直线对称的性质,求直线MN的方程是解题的难点.
(2)设出椭圆Cb的方程,直线lMN的方程,根据两点关于直线对称的性质,求出直线lMN的方程,根据直线lMN与椭圆Cb有两个不同的交点,判别式大于零,求得实数b的取值范围.
(3)作法:过原点作直线y=kx(k≠1),交椭圆M和椭圆Mλ于点E和点F,则△CDF和△ABE即为所求相似三角形,且相似比为λ.
解答:解:(1)椭圆C2与C1相似. 因为椭圆C2的特征三角形是腰长为a=4,底边长为2c=
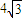 的等腰三角形,
的等腰三角形,而椭圆C1的特征三角形是腰长为2,底边长为
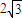 的等腰三角形,因此两个等腰三角形相似,且相似比为2.
的等腰三角形,因此两个等腰三角形相似,且相似比为2.(2)椭圆Cb的方程为:
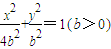 ,
,设lMN:y=-x+t,点M(x1,y1),N(x2,y2),MN中点为(x,y),
则
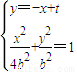 ,所以5x2-8tx+4(t2-b2)=0,则
,所以5x2-8tx+4(t2-b2)=0,则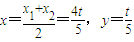 .
.因为中点在直线y=x+1上,所以有
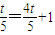 ,
,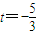 ,即直线lMN的方程为:
,即直线lMN的方程为: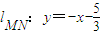 ,
,由题意可知,直线lMN与椭圆Cb有两个不同的交点,
即方程
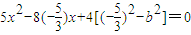 有两个不同的实数解,
有两个不同的实数解,所以
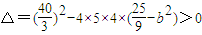 ,即
,即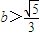 .
.(3)作法:过原点作直线y=kx(k≠1),交椭圆M和椭圆Mλ于点E和点F,则△CDF和△ABE即为所求相似三角形,且相似比为λ.
点评:本题考查直线和圆锥曲线的位置关系,两点关于直线对称的性质,求直线MN的方程是解题的难点.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆 (2011•徐汇区三模)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆
(2011•徐汇区三模)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆 。
。
 ,判断
,判断 与
与 是否相似?如果相似,求出
是否相似?如果相似,求出 的椭圆
的椭圆 的方程;若在椭圆
的方程;若在椭圆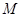 、
、 关于直线
关于直线 对称,求实数
对称,求实数 与两个“相似椭圆”
与两个“相似椭圆” 和
和 分别交于点
分别交于点 和点
和点 ,证明:
,证明: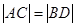
 .
. ,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由;
,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由; 和
和 分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
 .
. ,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由;
,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由; 和
和 分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)