题目内容
双曲线 的虚轴端点与一个焦点连线的中点恰在双曲线的一条准线上,PQ是双曲线的一条垂直于实轴的弦,o为坐标原点,则
的虚轴端点与一个焦点连线的中点恰在双曲线的一条准线上,PQ是双曲线的一条垂直于实轴的弦,o为坐标原点,则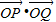 等于( )
等于( )A.0
B.-1
C.1
D.与PQ的位置及a的值有关
【答案】分析:由双曲线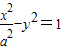 的虚轴端点与一个焦点连线的中点恰在双曲线的一条准线上,能够推导出a2=3.再利用双曲线的性质和向量的娄得积公式能够推导出
的虚轴端点与一个焦点连线的中点恰在双曲线的一条准线上,能够推导出a2=3.再利用双曲线的性质和向量的娄得积公式能够推导出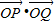 .
.
解答:解:取双曲线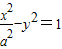 的虚轴端点B(1,0)与焦点F(
的虚轴端点B(1,0)与焦点F(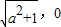 ),则BP的中点坐标的横坐标
),则BP的中点坐标的横坐标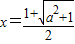 ,
,
∵BP的中点在双曲线的准线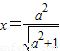 上,∴
上,∴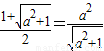 .解得a2=3.
.解得a2=3.
∵PQ是双曲线的一条垂直于实轴的弦,
∴可设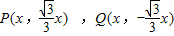 ,则
,则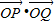 =
=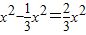 .
.
故选D.
点评:本题考查双曲线的端点坐标、准线方程和向量的数量积,在解题过程中要注意合理选取公式.
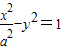 的虚轴端点与一个焦点连线的中点恰在双曲线的一条准线上,能够推导出a2=3.再利用双曲线的性质和向量的娄得积公式能够推导出
的虚轴端点与一个焦点连线的中点恰在双曲线的一条准线上,能够推导出a2=3.再利用双曲线的性质和向量的娄得积公式能够推导出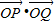 .
.解答:解:取双曲线
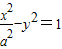 的虚轴端点B(1,0)与焦点F(
的虚轴端点B(1,0)与焦点F(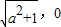 ),则BP的中点坐标的横坐标
),则BP的中点坐标的横坐标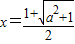 ,
,∵BP的中点在双曲线的准线
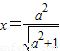 上,∴
上,∴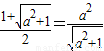 .解得a2=3.
.解得a2=3.∵PQ是双曲线的一条垂直于实轴的弦,
∴可设
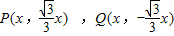 ,则
,则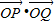 =
=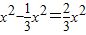 .
.故选D.
点评:本题考查双曲线的端点坐标、准线方程和向量的数量积,在解题过程中要注意合理选取公式.

练习册系列答案
相关题目