题目内容
△ABC的外接圆的直径为1,三个内角A、B、C的对边为a、b、c,| m |
| n |
| m |
| n |
(1)求sinA+sinB的取值范围;
(2)若abx=a+b,试确定实数x的取值范围.
分析:(1)通过
⊥
推出acosA-bcosB=0,结合正弦定理化简此式,推出A,B的关系,然后求sinA+sinB的取值范围;
(2)利用abx=a+b,结合正弦定理,推出x的表达式,利用换元法,结合函数的单调性,试确定实数x的取值范围.
| m |
| n |
(2)利用abx=a+b,结合正弦定理,推出x的表达式,利用换元法,结合函数的单调性,试确定实数x的取值范围.
解答:解:(1)∵
⊥
,∴
•
=0,∴acosA-bcosB=0.
由正弦定理知,
=
=2R=1,∴a=sinA,b=sinB.
∴sinAcosA=sinBcosB,∴sin2A=sin2B.
∵A,B∈(0,π),∴2A=2B或2A+2B=π.
∴A=B,A+B=
.sinA+sinB=sinA+cosA=
sin(A+
),
<A+
<
,
∴
<sin(A+
)≤1.
∴sinA+sinB的取值范围为(1,
].
(2)∵abx=a+b,∴sinA•sinB•x=sinA+sinB
∴x=
.
令sinA+cosA=t∈(1,
],sinAcosA=
,
∴x=
=
.
∵t-
在(1,
]单调递增,∴0<t-
≤
-
=
,
∴x≥2
,故x的取值范围为[2
,+∞).
| m |
| n |
| m |
| n |
由正弦定理知,
| a |
| sinA |
| b |
| sinB |
∴sinAcosA=sinBcosB,∴sin2A=sin2B.
∵A,B∈(0,π),∴2A=2B或2A+2B=π.
∴A=B,A+B=
| π |
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴
| ||
| 2 |
| π |
| 4 |
∴sinA+sinB的取值范围为(1,
| 2 |
(2)∵abx=a+b,∴sinA•sinB•x=sinA+sinB
∴x=
| sinA+cosA |
| sinAcosA |
令sinA+cosA=t∈(1,
| 2 |
| t2-1 |
| 2 |
∴x=
| 2t |
| t2-1 |
| 2 | ||
t-
|
∵t-
| 1 |
| t |
| 2 |
| 1 |
| t |
| 2 |
| 1 | ||
|
| ||
| 2 |
∴x≥2
| 2 |
| 2 |
点评:本题是中档题,考查正弦定理的应用,三角函数的最值,注意换元法的应用,函数的单调性是求最值的一种方法,考查计算能力,转化思想.

练习册系列答案
相关题目
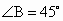 ,△ABC的面积S=2,那么△ABC的外接圆的直长等于________.
,△ABC的面积S=2,那么△ABC的外接圆的直长等于________.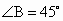 ,△ABC的面积S=2,那么△ABC的外接圆的直长等于________.
,△ABC的面积S=2,那么△ABC的外接圆的直长等于________.