题目内容
不等式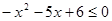 的解集为( )
的解集为( )
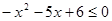 的解集为( )
的解集为( )A.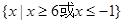 | B. |
C. | D. |
D
分析:根据不等式的基本性质在不等式两边都除以-1,不等号方向改变,因式分解后转化为x-1与x+6同号,即可求出原不等式的解集.
解答:解:原不等式可化为:x2+5x-6≥0,
因式分解得:(x-1)(x+6)≥0,
即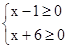
或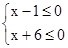 ,
,
解得:x≥1或x≤-6,
所以原不等式的解集为:{x|x≤-6或x≥1}.
故选D
解答:解:原不等式可化为:x2+5x-6≥0,
因式分解得:(x-1)(x+6)≥0,
即
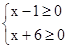
或
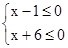 ,
,解得:x≥1或x≤-6,
所以原不等式的解集为:{x|x≤-6或x≥1}.
故选D

练习册系列答案
相关题目
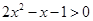 的解集是 ( )
的解集是 ( )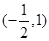
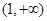
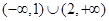
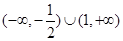
 的不等式
的不等式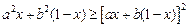
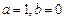 时解不等式;
时解不等式;
 ,
,  解不等式.
解不等式.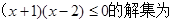 ()
()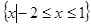
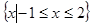
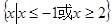
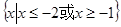
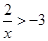 的解集是( )
的解集是( )



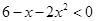 的解集是( )
的解集是( )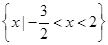
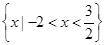
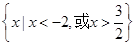
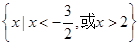
 的解集是 。
的解集是 。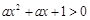 对一切
对一切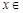 R恒成立,则实数
R恒成立,则实数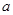 的取值范围是
的取值范围是