题目内容
设全集U={1,2},集合A={x|x2+px+q=0},CUA={1},
(1)求p、q;
(2)试求函数y=px2+qx+15在[ ,2]上的反函数.
,2]上的反函数.
解:(1)∵U={1,2},而CUA={1},
∴A={2},即方程x2+px+q=0的两根均为2,
由一元二次方程根与系数的关系知: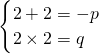 ,∴
,∴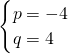 .
.
(2)∵y=-4x2+4x+15=-4(x- )2+16,
)2+16,
而 ≤x≤2,∴7≤y≤16,
≤x≤2,∴7≤y≤16,
∴4(x- )2=16-y,
)2=16-y,
∴x- =
=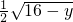 ,
,
∴x= +
+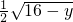 ,
,
故原函数的反函数是y= +
+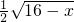 (7≤x≤16).
(7≤x≤16).
分析:(1)根据集合U和集合CUA,得出集合A={2},说明方程x2+px+q=0有两个相等的实数根且均为2,可以用一元二次方程根与系数的关系求出的p、q值;
(2)在(1)的条件下得函数y=px2+qx+15就是y=-4x2+4x+15,将其看成关于x的方程解出x=φ(y)的表达式,再根据x的取值范围进行取舍得出x= +
+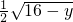 ,最后将x、y进行互换,可得函数y=px2+qx+15在[
,最后将x、y进行互换,可得函数y=px2+qx+15在[ ,2]上的反函数.
,2]上的反函数.
点评:本题考查了一元二次方程根与系数的关系、以及集合关系中的参数取值等问题.同时还考查了反函数的求法,在求反函数的同时请注意还要注明反函数自变量的取值
范围.
∴A={2},即方程x2+px+q=0的两根均为2,
由一元二次方程根与系数的关系知:
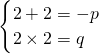 ,∴
,∴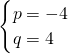 .
.(2)∵y=-4x2+4x+15=-4(x-
 )2+16,
)2+16,而
 ≤x≤2,∴7≤y≤16,
≤x≤2,∴7≤y≤16,∴4(x-
 )2=16-y,
)2=16-y,∴x-
 =
=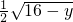 ,
,∴x=
 +
+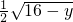 ,
,故原函数的反函数是y=
 +
+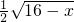 (7≤x≤16).
(7≤x≤16).分析:(1)根据集合U和集合CUA,得出集合A={2},说明方程x2+px+q=0有两个相等的实数根且均为2,可以用一元二次方程根与系数的关系求出的p、q值;
(2)在(1)的条件下得函数y=px2+qx+15就是y=-4x2+4x+15,将其看成关于x的方程解出x=φ(y)的表达式,再根据x的取值范围进行取舍得出x=
 +
+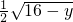 ,最后将x、y进行互换,可得函数y=px2+qx+15在[
,最后将x、y进行互换,可得函数y=px2+qx+15在[ ,2]上的反函数.
,2]上的反函数.点评:本题考查了一元二次方程根与系数的关系、以及集合关系中的参数取值等问题.同时还考查了反函数的求法,在求反函数的同时请注意还要注明反函数自变量的取值
范围.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目