题目内容
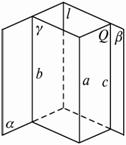
求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.
分析:利用线面平行的性质定理及平行公理即可得出结论.
解答:已知:如图,α∩β=b,a∥α,a∥β.求证:a∥b.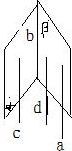
证明:由a∥α得,经过a的平面与α相交于直线c,
则a∥c,
同理,设经过a的平面与β相交于直线d,
则a∥d,由平行公理得:c∥d,
则c∥β,又c?α,α∩β=b,所以c∥b,
又a∥c,所以a∥b.

证明:由a∥α得,经过a的平面与α相交于直线c,
则a∥c,
同理,设经过a的平面与β相交于直线d,
则a∥d,由平行公理得:c∥d,
则c∥β,又c?α,α∩β=b,所以c∥b,
又a∥c,所以a∥b.
点评:本题考查线面平行的判定与性质定理及平行公理,要注意线面平行的判定与性质的综合应用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目