题目内容
某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米),并把这些高度列成了如下的频数分布表:| 分 组 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频 数 | 2 | 3 | 14 | 15 | 12 | 4 |
(2)这批树苗的平均高度大约是多少?(计算时用各组的中间值代替各组数据的平均值);
(3)为了进一步获得研究资料,若从[40,50)组中移出一棵树苗,从[90,100]组中移出两棵树苗进行试验研究,则[40,50)组中的树苗A和[90,100]组中的树苗C同时被移出的概率是多少?
【答案】分析:(1)根据题意,由频率分布表可得高度不低于80厘米的频数,进而由等可能事件的概率公式,计算可得答案;
(2)首先计算出样本容量,进而由平均数的计算公式计算可得答案;
(3)设[40,50)组中的树苗为A、B,[90,100]组中的树苗为C、D、E、F,用列表法可得移出3棵树苗的基本事件的数目与A、C同时被移出的事件数目,有等可能事件的概率公式计算可得答案.
解答:解:(I)∵高度不低于80厘米的频数是12+4=16,
∴高度不低于80厘米树苗的概率为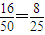 .
.
(2)根据题意,样本容量即各组频数之和为2+3+14+15+12+4=50,
则树苗的平均高度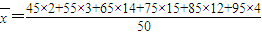 =
=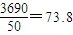 cm;
cm;
(3)设[40,50)组中的树苗为A、B,[90,100]组中的树苗为C、D、E、F,
则基本事件总数为12,它们是:ACD、ACE、ACF、ADE、ADF、AEF、BCD、BCE、BCF、BDE、BDF、BEF,
而满足A、C同时被移出的事件为ACD、ACE、ACF共3种,
∴树苗A和树苗C同时被移出的概率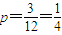 .
.
点评:本题考查频率分布表的应用,涉及等可能事件的概率的计算,注意从频率分布表中分析出要求的数据及信息.
(2)首先计算出样本容量,进而由平均数的计算公式计算可得答案;
(3)设[40,50)组中的树苗为A、B,[90,100]组中的树苗为C、D、E、F,用列表法可得移出3棵树苗的基本事件的数目与A、C同时被移出的事件数目,有等可能事件的概率公式计算可得答案.
解答:解:(I)∵高度不低于80厘米的频数是12+4=16,
∴高度不低于80厘米树苗的概率为
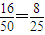 .
.(2)根据题意,样本容量即各组频数之和为2+3+14+15+12+4=50,
则树苗的平均高度
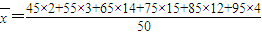 =
=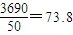 cm;
cm;(3)设[40,50)组中的树苗为A、B,[90,100]组中的树苗为C、D、E、F,
则基本事件总数为12,它们是:ACD、ACE、ACF、ADE、ADF、AEF、BCD、BCE、BCF、BDE、BDF、BEF,
而满足A、C同时被移出的事件为ACD、ACE、ACF共3种,
∴树苗A和树苗C同时被移出的概率
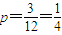 .
.点评:本题考查频率分布表的应用,涉及等可能事件的概率的计算,注意从频率分布表中分析出要求的数据及信息.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(本小题满分14分)
某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米),并把这些高度列成了如下的频数分布表:
|
分 组 |
[40 , 50) |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90 , 100] |
|
频 数 |
2 |
3 |
14 |
15 |
12 |
4 |
(1) 在这批树苗中任取一棵,其高度不低于80厘米的概率是多少?
(2)这批树苗的平均高度大约是多少?(计算时用各组的中间值代替各组数据的平均值);
(3)为了进一步获得研究资料,若从[40,50)组中移出一棵树苗,从[90,100]组中移出两棵树苗进行试验研究,则[40 ,50)组中的树苗A和[90,100]组中的树苗C同时被移出的概率是多少?
某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米),并把这些高度列成了如下的频数分布表:
(1)在这批树苗中任取一棵,其高度不低于80厘米的概率是多少?
(2)这批树苗的平均高度大约是多少?(计算时用各组的中间值代替各组数据的平均值);
(3)为了进一步获得研究资料,若从[40,50)组中移出一棵树苗,从[90,100]组中移出两棵树苗进行试验研究,则[40,50)组中的树苗A和[90,100]组中的树苗C同时被移出的概率是多少?
| 分 组 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频 数 | 2 | 3 | 14 | 15 | 12 | 4 |
(2)这批树苗的平均高度大约是多少?(计算时用各组的中间值代替各组数据的平均值);
(3)为了进一步获得研究资料,若从[40,50)组中移出一棵树苗,从[90,100]组中移出两棵树苗进行试验研究,则[40,50)组中的树苗A和[90,100]组中的树苗C同时被移出的概率是多少?

 组中移出一棵树苗,从
组中移出一棵树苗,从 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则