题目内容
右图为某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.沿图中虚线将它们折叠起来,使P、Q、R、S四点重合于D1,这个几何体的体积为 ,需要 个这样的几何体才能拼成一个棱长为6的正方体.
【答案】分析:根据题意将图形折叠起来,画其直观图为一个有一条侧棱垂直于底面的四棱锥,然后利用棱锥的体积公式可求得其体积;画出棱长为6的正方体,找出四棱锥的个数即可.
解答: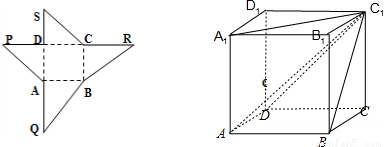 解:它是有一条侧棱垂直于底面的四棱锥(如图).(注:评分注意实线、虚线;垂直关系;长度比例等)
解:它是有一条侧棱垂直于底面的四棱锥(如图).(注:评分注意实线、虚线;垂直关系;长度比例等)
PD⊥AD,PD⊥CD,
∴PD⊥平面ABCD,则VP-ABCD= ×6×6×6=72
×6×6×6=72
需要3个这样的几何体可以拼成一个正方体.就是C1-ABCD,C1-A1B1BA,C1-ADD1A1;三个四棱锥.
故答案为:72;3.
点评:本题是基础题,考查几何体的体积的计算,考查空间想象能力.
解答:
 解:它是有一条侧棱垂直于底面的四棱锥(如图).(注:评分注意实线、虚线;垂直关系;长度比例等)
解:它是有一条侧棱垂直于底面的四棱锥(如图).(注:评分注意实线、虚线;垂直关系;长度比例等)PD⊥AD,PD⊥CD,
∴PD⊥平面ABCD,则VP-ABCD=
 ×6×6×6=72
×6×6×6=72需要3个这样的几何体可以拼成一个正方体.就是C1-ABCD,C1-A1B1BA,C1-ADD1A1;三个四棱锥.
故答案为:72;3.
点评:本题是基础题,考查几何体的体积的计算,考查空间想象能力.

练习册系列答案
相关题目
 右图为某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.沿图中虚线将它们折叠起来,使P、Q、R、S四点重合于D1,这个几何体的体积为
右图为某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.沿图中虚线将它们折叠起来,使P、Q、R、S四点重合于D1,这个几何体的体积为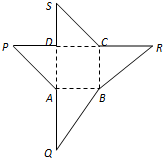 如图为某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.
如图为某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.
 右图为某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.沿图中虚线将它们折叠起来,使P、Q、R、S四点重合于D1,这个几何体的体积为________,需要________个这样的几何体才能拼成一个棱长为6的正方体.
右图为某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.沿图中虚线将它们折叠起来,使P、Q、R、S四点重合于D1,这个几何体的体积为________,需要________个这样的几何体才能拼成一个棱长为6的正方体.