题目内容
已知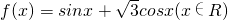
（1）求函数f（x）的最小正周期；
（2）求函数f（x）的最大值，并指出此时x的值．
解：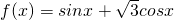
=2sin（x+
）
（1）函数f（x）的最小正周期：T=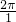
=2π．
（2）函数f（x）=2sin（x+）≤2，所以函数的最大值为：2；
此时x+=2k
，k∈Z，即x=
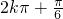，k∈Z
分析：（1）利用两角和的正弦函数化简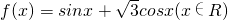，直接求函数f（x）的最小正周期；
（2）结合正弦函数的最值，求函数f（x）的最大值，并指出此时x的值．
点评：本题是基础题，考查三角函数的化简，周期的求法，最值的求法等基本知识，考查计算能力．
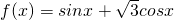=2sin（x+）（1）函数f（x）的最小正周期：T=
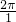=2π．（2）函数f（x）=2sin（x+
）≤2，所以函数的最大值为：2；此时x+
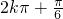=2k，k∈Z，即x=，k∈Z分析：（1）利用两角和的正弦函数化简
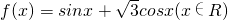，直接求函数f（x）的最小正周期；（2）结合正弦函数的最值，求函数f（x）的最大值，并指出此时x的值．
点评：本题是基础题，考查三角函数的化简，周期的求法，最值的求法等基本知识，考查计算能力．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
上的值域。
，若不等式f（a1）+f（a2）+f（a3）+…+f（a2009）≤x-ln（x-p）在x∈（p，+∞）时恒成立，求实数p的最小值．