题目内容
已知| C | 2 n+1 |
| C | 2 n |
| C | 3 n |
分析:本题中给的是一个关于组合数的方程,利用组合数公式展开成关于n的方程,解方程求n
解答:解:∵Cn+12-Cn2=Cn3,
∴
-
=
∴3n+3-3n+3=n2-3n+2
∴n2-3n-4=0
解得n=4
故答案为:4.
∴
| n(n+1) |
| 2 |
| n(n-1) |
| 2 |
| n(n-1)(n-2) |
| 3×2 |
∴3n+3-3n+3=n2-3n+2
∴n2-3n-4=0
解得n=4
故答案为:4.
点评:本题考查组合及组合数公式,解题的关键是熟练掌握组合数公式,能用公式将方程化简为一元二次方程

练习册系列答案
相关题目
已知
+1,m,
-1成等比数列,则m的值是( )
| 2 |
| 2 |
| A、1 | ||
| B、-1 | ||
| C、±1 | ||
D、
|
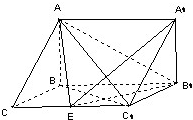 如图,在三棱柱△ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,BB1=2,∠BCC1=
如图,在三棱柱△ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,BB1=2,∠BCC1=