题目内容

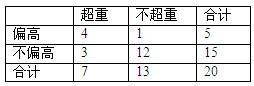
某研究小组为了研究中学生的身体发育情况，在学校随机抽出20名学生，将他们的身高和体重制成如下所示的2×2列联表：

	超重	不超重	合计
偏高	4	1	5
不偏高	3	12	15
合计	7	13	20

（1）在超重的学生中取两个，求一个偏高一个不偏高的概率；
（2）根据联表可有多大把握认为身高与体重有关系？

P（K²≥k）	0.025	0.010	0.005	0.001
k	5.024	6.635	7.879	10.828

分析：（1）由题意知本题是一个等可能事件的概率，由表格数据可知偏高4人和不偏高3人，总共7人，利用组合数写出所有的基本事件数及，一个偏高一个不偏高的事件数，得到概率；
（2）这是一个独立性检验应用题，处理本题时可根据列联表，及K²的计算公式，计算出K²的值，并代入临界值表中进行比较，不难得到答案．

解答：解：（1）在超重的7个学生中取两个，共有C

=21种，
一个偏高一个不偏高的有4×3=12，
∴在超重的学生中取两个，一个偏高一个不偏高的概率

．
（2）由于

则K²=

20(4×12-1×3)2

7×13×5×15

≈5.934＞5.024
故有97.5%的把握认为该学校的男生的身高和体重之间有关系．

点评：本题主要考查了古典概型及其概率计算公式、独立性检验，属于基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

组序	分组	频数	频率
第一组	[180，210）	5	0.1
第二组	[210，240）	10	0.2
第三组	[240，270）	12	0.24
第四组	[270，300）	a	b
第五组	[300，330）	6	c

（1）求表中的a、b、c的值；
（2）某课题小组为了研究自主学习时间与成绩的相关性，需用分层抽样方法，从这50名学生中随机抽取20名作统计分析，求在第二组学生中应抽取多少人？
（3）已知第一组学生中有3名男生和2名女生，从这5名学生中随机抽取2人，求恰好抽到1名男生和1名女生的概率．

（本题满分14分）某研究小组为了研究学生的数学成绩与物理成绩之间的关系，随机抽取高二年级20名学生某次考试的成绩（百分制）如下表所示：

序号	1	2	3	4	5	6	7	8	9	10
数学成绩	95	75	80	94	92	65	67	84	98	71
物理成绩	90	63	72	87	91	71	58	82	93	80
序号	11	12	13	14	15	16	17	18	19	20
数学成绩	67	93	64	78	77	90	57	84	72	83
物理成绩	77	82	48	85	69	91	61	82	78	86

若数学成绩90分（含90分）以上为优秀，物理成绩85分（含85分）以上为优秀。

⑴根据上表完成下面的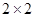列联表：

	数学成绩优秀	数学成绩不优秀	合计
物理成绩优秀
物理成绩不优秀		12
合计			20

⑵根据⑴中表格的数据计算，有多少的把握，认为学生的数学成绩与物理成绩之间有关系？

某研究小组为了研究中学生的身体发育情况，在学校随机抽出20名学生，将他们的身高和体重制成如下所示的2×2列联表：
超重不超重合计
偏高 4 1 5
不偏高 3 12 15
合计 7 13 20
（1）在超重的学生中取两个，求一个偏高一个不偏高的概率；
（2）根据联表可有多大把握认为身高与体重有关系？
P（K²≥k） 0.025 0.010 0.005 0.001
k 5.024 6.635 7.879 10.828

某研究小组为了研究中学生的身体发育情况，在学校随机抽出20名学生，将他们的身高和体重制成如下所示的2×2列联表：

	超重	不超重	合计
偏高	4	1	5
不偏高	3	12	15
合计	7	13	20

（1）在超重的学生中取两个，求一个偏高一个不偏高的概率；
（2）根据联表可有多大把握认为身高与体重有关系？

P（K²≥k）	0.025	0.010	0.005	0.001
k	5.024	6.635	7.879	10.828

试题分类