题目内容
现有200根相同的钢管,把它们堆放成正三角形垛,要使剩余的钢管尽可能的少,那么剩余钢管的根数为( )
A.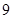 | B.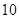 | C.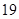 | D.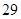 |
B
由题意可知正三角形垛各层的钢管数组成一个首项为1,公差是1的数列,由此得Sn="n(n+1)/" 2<200.解出使不等式成立的n的最大值,再求剩余的钢管数即可选出正确选项
解:∵把200根相同的圆钢管堆放成一个正三角形垛,
∴正三角形垛各层的钢管数组成一个首项为1,公差是1的数列,
∴正三角形垛所需钢总数为Sn=1+2+3+4+…+n=n(n+1)/2,
令 Sn=n(n+1)/2<200,
解得n=19是使得不等式成立的最大整数,此时Sn取最大值190,由此可以推出剩余的钢管有10根.
故选B.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
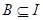 ,若A中含有3个元素,B中至少含有2个元素,且B中所有数均不小于A中最大的数,则满足条件的集合A、B有( )
,若A中含有3个元素,B中至少含有2个元素,且B中所有数均不小于A中最大的数,则满足条件的集合A、B有( )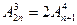 ,则
,则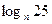 的值为( )
的值为( )
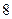 人,从男生中选
人,从男生中选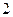 人,从女生中选
人,从女生中选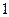 人分别参加数学、
人分别参加数学、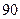 种不同方案,那么男、女生人数分别是( ).
种不同方案,那么男、女生人数分别是( ).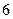 人
人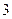 人,女生
人,女生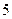 人
人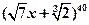 的展开式中所得
的展开式中所得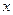 的多项式中,系数为有理数的项共有( )
的多项式中,系数为有理数的项共有( )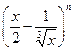 各项展开式的二项式系数之和为
各项展开式的二项式系数之和为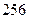 .
.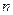 ;
;