题目内容
设二次函数 在区间
在区间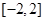 上的最大值、最小值分别是
上的最大值、最小值分别是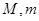 ,集合
,集合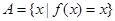 .
.
(Ⅰ)若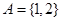 ,且
,且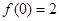 ,求
,求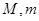 的值;
的值;
(Ⅱ)若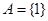 ,且
,且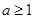 ,记
,记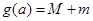 ,求
,求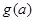 的最小值.
的最小值.
【答案】
(Ⅰ)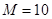 ,
,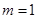 ;(Ⅱ)
;(Ⅱ)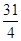 .
.
【解析】
试题分析:(Ⅰ)由方程的根求出函数解析式,再利用函数的单调性求出最值;(Ⅱ)由方程有两相等实根1,求出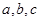 的关系式,消去
的关系式,消去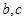 得到含有参数
得到含有参数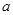 函数解析式,进一步求出
函数解析式,进一步求出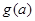 ,再由
,再由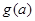 的单调性求出最小值.
的单调性求出最小值.
试题解析:(Ⅰ)由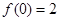 ,可知
,可知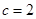 1分
1分
又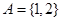 ,故1和2是方程
,故1和2是方程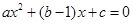 的两实根,所以
的两实根,所以
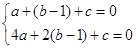 3分 解得,
3分 解得,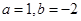 4分
4分
所以,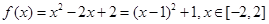
当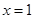 时
时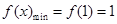 ,即
,即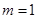 5分
5分
当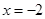 时
时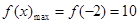 ,即
,即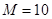 6分
6分
(Ⅱ)由题意知方程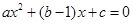 有两相等实根1,所以
有两相等实根1,所以
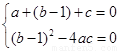 ,即
,即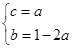 ,
8分
,
8分
所以,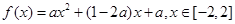
其对称轴方程为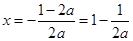 ,
,
又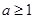 ,故
,故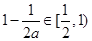 9分
9分
所以,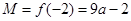 10分
10分
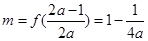 11分
11分
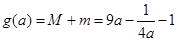 14分
14分
又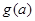 在
在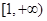 单调递增,所以当
单调递增,所以当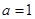 时,
时,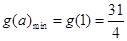 16分
16分
考点:二次函数的解析式、二次函数在闭区间上的最值,函数的单调性.

练习册系列答案
相关题目
 在区间
在区间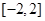 上的最大值、最小值分别是
上的最大值、最小值分别是 ,集合
,集合 .
.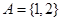 ,且
,且 ,求
,求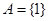 ,且
,且 ,记
,记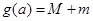 ,求
,求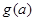 的最小值.
的最小值.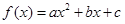 在区间
在区间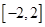 上的最大值、最小值分别是
上的最大值、最小值分别是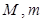 ,集合
,集合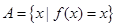 .
. 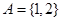 ,且
,且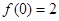 ,求
,求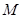 和
和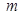 的值;
的值;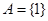 ,且
,且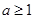 ,记
,记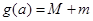 ,求
,求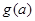 的最小值.
的最小值.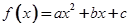 在区间
在区间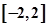 上的最大值、最小值分别是M、m,集合
上的最大值、最小值分别是M、m,集合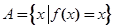 .
. 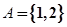 ,且
,且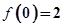 ,求M和m的值;
,求M和m的值;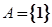 ,且
,且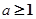 ,记
,记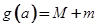 ,求
,求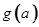 的最小值.
的最小值.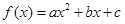 在区间
在区间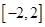 上的最大值、最小值分别是M、m,集合
上的最大值、最小值分别是M、m,集合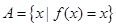 .若
.若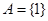 ,且
,且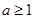 ,记
,记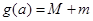 ,则
,则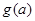 的最小值 。
的最小值 。