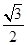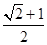题目内容
在正三棱锥
中，
、
分别是棱
、
的中点，且
，若侧棱
，则正三棱锥外接球的表面积是（ ）
A． | B． | C． | D． |
C
解析试题分析：∵三棱锥为正棱锥，∴
⊥
，∴
⊥．
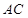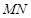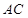又∵⊥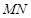
，
，
∴
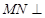平面
，即⊥平面，
∴
，将此三棱锥补成正方体，则它们有相同的外接球，
∴
，解得
，∴
．
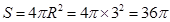考点：三棱锥的外接球表面积．
练习册系列答案
优等生题库系列答案
相关题目
一简单组合体的三视图如图（1）所示，则该组合体的体积为（ ）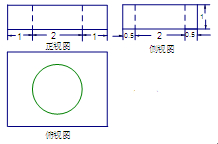
A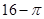． | B． | C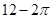． | D． |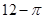
某几何体的三视图如图所示（单位：cm），则该几何体的体积是( )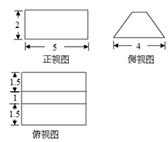
A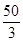．  | B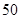． | C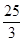． | D． |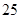
某几何体的三视图如图所示，则该几何体的体积为（ ）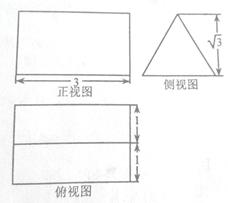
| A．6 | B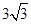． | C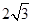． | D．3 |
已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为V1，直径为4的球的体积为V2，则V1:V2等于（ ）
| A．1:2 |
| B．2:1 |
| C．1:1 |
| D．1:4 |
如图所示,正方体ABCD
A1B1C1D1的棱长为2,动点E,F在棱A1B1上,点Q是棱CD的中点,动点P在棱AD上.若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥PEFQ的体积( )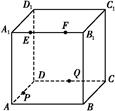
| A．与x,y都有关 |
| B．与x,y都无关 |
| C．与x有关,与y无关 |
| D．与y有关,与x无关 |
一个简单几何体的主视图、俯视图如图所示，则其左视图不可能为( )
| A．正方形 | B．圆 |
| C．等腰三角形 | D．直角梯形 |
已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为V1，直径为4的球的体积为V2，则( )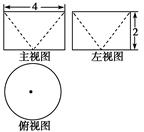
| A．1∶2 | B．2∶1 | C．1∶1 | D．1∶4 |
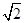的矩形，则该正方体的正视图的面积等于( )
