题目内容
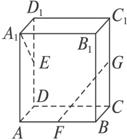
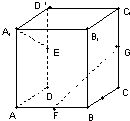 如图长方体ABCD-A1B1C1D1中,AA1=AB=4,AD=2,E、F、G分别是DD1、AB、CC1的中点,则直线A1E,FG所夹的角的余弦值为
如图长方体ABCD-A1B1C1D1中,AA1=AB=4,AD=2,E、F、G分别是DD1、AB、CC1的中点,则直线A1E,FG所夹的角的余弦值为0
0
.分析:根据异面直线所成角的定义求解.
解答:解:建立以D点为坐标原点,以DA,DC,DD1,分别为x,y,z轴的空间直角坐标系.
则A(2,0,0),A1 (2,0,4),
因为E、F、G分别是DD1、AB、CC1的中点,
所以E(0,0,2),F(2,2,0),G(0,4,2),
所以
=(-2,0,-2),
=(-2,2,2),
因为
?
=(-2,0,-2)?(-2,2,2)=-2×(-2)-2×2=0,
所以
⊥
,即A1E⊥FG,
所以直线A1E,FG所夹的角为90°,所以cos90°=0.
故答案为:0.
则A(2,0,0),A1 (2,0,4),
因为E、F、G分别是DD1、AB、CC1的中点,
所以E(0,0,2),F(2,2,0),G(0,4,2),
所以
| A1E |
| FG |
因为
| A1E |
| FG |
所以
| A1E |
| FG |
所以直线A1E,FG所夹的角为90°,所以cos90°=0.
故答案为:0.
点评:本题主要考查异面直线所成角的求法,利用向量法和坐标法是解决空间夹角中,最常用的方法.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目