题目内容
已知椭圆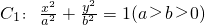 过点
过点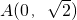 且它的离心率为
且它的离心率为 .
.
(1)求椭圆C1的方程;
(2)设椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直l1于点P,线段PF2的垂直平分线交l2于点M,求点M的轨迹C2的方程;
(3)已知动直线l过点Q(4,0),交轨迹C2于R、S两点.是否存在垂直于x轴的直线m被以RQ为直径的圆O1所截得的弦长恒为定值?如果存在,求出m的方程;如果不存在,说明理由.
解:(1)因为椭圆 (a>b>0)过点
(a>b>0)过点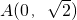 ,所以
,所以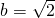 ,b2=2,
,b2=2,
又因为椭圆C1的离心率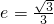 ,所以
,所以 ,解得a2=3.
,解得a2=3.
所以椭圆C1的方程是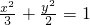 ;
;
(2)因为线段PF2的垂直平分线交l2于点M,
所以|MP|=|MF2|,即动点M到定直线l1:x=-1的距离等于它到定点F2(1,0)的距离,
所以动点M的轨迹C2是以l1为准线,F2为焦点的抛物线,
所以点M的轨迹C2的方程为y2=4x;
(3)设R(x1,y1),假设存在直线m:x=t满足题意,则圆心 ,
,
过O1作直线x=t的垂线,垂足为E,设直线m与圆O1的一个交点为G.
可得: ,
,
即
=
=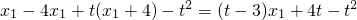 ,
,
当t=3时,|EG|2=3,此时直线m被以RQ为直径的圆O1所截得的弦长恒为定值 .
.
因此存在直线m:x=3满足题意.
分析:(1)根据椭圆所过点A可求得b值,再由离心率及a2=b2+c2即可求得a值,
(2)由题意可知|MP|=|MF2|,即动点M到定直线l1:x=-1的距离等于它到定点F2(1,0)的距离,从而可判断动点M的轨迹为抛物线,进而可求得其方程;
(3)设R(x1,y1),假设存在直线m:x=t满足题意,可表示出圆O1的方程,过O1作直线x=t的垂线,垂足为E,设直线m与圆O1的一个交点为G.利用勾股定理可用t,x1表示出|EG|2,根据表达式可求得t值满足条件.
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查学生对问题的探究能力解决问题的能力,(2)问的解决基础是掌握抛物线的定义,(3)问探究问题的处理方法往往是先假设存在,然后由条件进行推导,如满足条件即存在,否则不然.
 (a>b>0)过点
(a>b>0)过点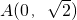 ,所以
,所以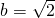 ,b2=2,
,b2=2,又因为椭圆C1的离心率
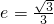 ,所以
,所以 ,解得a2=3.
,解得a2=3.所以椭圆C1的方程是
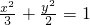 ;
;(2)因为线段PF2的垂直平分线交l2于点M,
所以|MP|=|MF2|,即动点M到定直线l1:x=-1的距离等于它到定点F2(1,0)的距离,
所以动点M的轨迹C2是以l1为准线,F2为焦点的抛物线,
所以点M的轨迹C2的方程为y2=4x;
(3)设R(x1,y1),假设存在直线m:x=t满足题意,则圆心
 ,
,过O1作直线x=t的垂线,垂足为E,设直线m与圆O1的一个交点为G.
可得:
 ,
,即

=

=
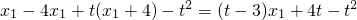 ,
,当t=3时,|EG|2=3,此时直线m被以RQ为直径的圆O1所截得的弦长恒为定值
 .
.因此存在直线m:x=3满足题意.
分析:(1)根据椭圆所过点A可求得b值,再由离心率及a2=b2+c2即可求得a值,
(2)由题意可知|MP|=|MF2|,即动点M到定直线l1:x=-1的距离等于它到定点F2(1,0)的距离,从而可判断动点M的轨迹为抛物线,进而可求得其方程;
(3)设R(x1,y1),假设存在直线m:x=t满足题意,可表示出圆O1的方程,过O1作直线x=t的垂线,垂足为E,设直线m与圆O1的一个交点为G.利用勾股定理可用t,x1表示出|EG|2,根据表达式可求得t值满足条件.
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查学生对问题的探究能力解决问题的能力,(2)问的解决基础是掌握抛物线的定义,(3)问探究问题的处理方法往往是先假设存在,然后由条件进行推导,如满足条件即存在,否则不然.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
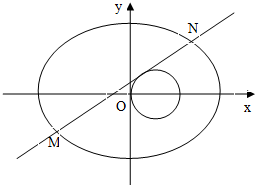 已知椭圆
已知椭圆 (2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率
(2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率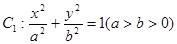 过点
过点 ,且它的离心率
,且它的离心率 .直线
.直线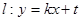 与椭圆
与椭圆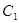 交于
交于 、
、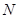 两点.
两点.
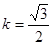 时,求证:
时,求证: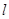 与圆
与圆 相切,椭圆上一点
相切,椭圆上一点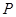 满足
满足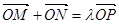 ,求实数
,求实数 的取值范围.
的取值范围.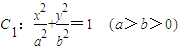 过点
过点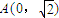 且它的离心率为
且它的离心率为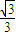 .
.