题目内容
设等差数列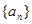 的前n项之和为
的前n项之和为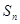 ,已知
,已知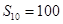 ,则
,则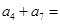 ( )
( )
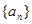 的前n项之和为
的前n项之和为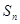 ,已知
,已知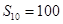 ,则
,则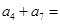 ( )
( )| A.12 | B.20 | C.40 | D.100 |
B
分析:要求a4+a7就要得到此等差数列的首项和公差,而已知S10=100,由等差数列的前n项和的通项公式可得到首项与公差的关系.代入求出即可。
解答:
由等差数列的前n项和的公式得:s10=10a1+10×9/2d=100,即2a1+9d=20;
而a4+a7=a1+3d+a1+6d=2a1+9d=20。
故选B。
点评:本题是一道基础计算题,要求学生会利用等差数列的通项公式及前n项和的公式进行化简求值,做题时学生应注意利用整体代换的数学思想解决数学问题。

练习册系列答案
相关题目
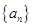 的前
的前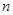 项和
项和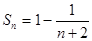 ,则
,则 的值是( )
的值是( )
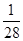
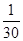

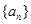 为等差数列,
为等差数列,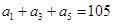 ,
,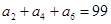 ,则
,则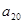 等于( )
等于( )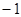
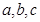 三数成等比数列,而
三数成等比数列,而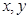 分别为
分别为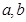 和
和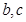 的等差中项,则
的等差中项,则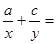 ( )
( )
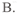
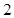 C.
C.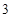 D.不确定
D.不确定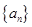 的前
的前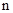 项和为
项和为 ,若
,若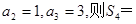 ( )
( )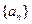 中,
中, 首项
首项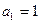 ,数列
,数列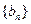 满足
满足 则数列
则数列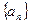 满足
满足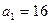 ,
,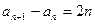 ,则
,则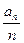 的最小值为
的最小值为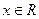 ,记不超过
,记不超过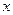 的最大整数为
的最大整数为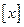 ,如
,如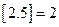 ,
,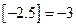 ,令
,令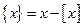 ,则
,则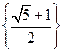 ,
,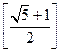 ,
,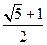 ,三个数构成的数列( )
,三个数构成的数列( )