题目内容
在等差数列{an}中an>0,且a1+a2+…+a10=30,则a5·a6的最大值等于 ( )
| A.3 | B.6 | C.9 | D.36 |
C
解析试题分析:因为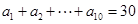 ,由等差数列性质得
,由等差数列性质得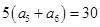 ,即
,即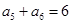 ,又
,又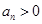 ,由基本不等式得
,由基本不等式得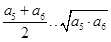 ,即
,即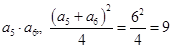 ,所以正确答案为C.
,所以正确答案为C.
考点:1.等差数列;2.基本不等式.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知 为等差数列,其公差为-2,且
为等差数列,其公差为-2,且 是
是 与
与 的等比中项,
的等比中项, 为
为 前
前 项和,
项和, 则
则 的值为( )
的值为( )
| A.-110 | B.-90 | C.90 | D.110 |
设函数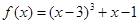 ,数列
,数列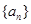 是公差不为0的等差数列,
是公差不为0的等差数列,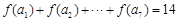 ,则
,则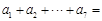 ( )
( )
| A.0 | B.7 | C.14 | D.21 |
已知数列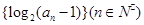 是等差数列,且
是等差数列,且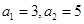 ,则
,则 ( )
( )
| A.2 | B.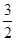 | C.1 | D.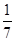 |
已知正实数数列 中,
中,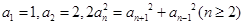 ,则
,则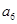 等于( )
等于( )
| A.16 | B.8 | C. | D.4 |
设等差数列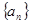 的前项和为
的前项和为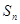 ,若
,若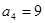 ,
,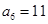 ,则
,则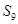 等于( )
等于( )
| A.180 | B.90 | C.72 | D.100 |
设 为等差数列,且
为等差数列,且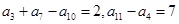 ,则数列
,则数列 的前13项的和为
的前13项的和为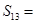
| A.63 | B.109 | C.117 | D.210 |
在等差数列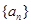 中,若
中,若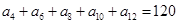 ,则
,则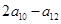 的值为( )
的值为( )
| A.20 | B.22 | C.24 | D.28 |
在等差数列{an}中,首项a1=0,公差d≠0,若am=a1+a2+…+a9,则m的值为( )
| A.37 | B. 36 | C.20 | D.19 |