题目内容
设函数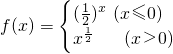 ,若f(x0)>2,则x0的取值范围是________.
,若f(x0)>2,则x0的取值范围是________.
(-∞,-1)∪(4,+∞)
分析:函数是分段函数,要分类讨论:①当x<2时,有2x>1,解出x的范围;②当x≥2时,有 >1,解出x的范围;然后综合①②从而求解.
>1,解出x的范围;然后综合①②从而求解.
解答:(1)当x0≤0时有,( )x0>2,解得x0<-1,
)x0>2,解得x0<-1,
∴x0<-1;
(2)当x0>0时,有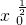 >2,
>2,
∴x0>4,
解得x0>4,
综合(1)(2)得x0∈(-∞,-1)∪(4,+∞)
故答案为:(-∞,-1)∪(4,+∞).
点评:此题考查分段函数的性质,要学会分类讨论,此题是一道很基础的题.
分析:函数是分段函数,要分类讨论:①当x<2时,有2x>1,解出x的范围;②当x≥2时,有
 >1,解出x的范围;然后综合①②从而求解.
>1,解出x的范围;然后综合①②从而求解.解答:(1)当x0≤0时有,(
 )x0>2,解得x0<-1,
)x0>2,解得x0<-1,∴x0<-1;
(2)当x0>0时,有
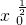 >2,
>2,∴x0>4,
解得x0>4,
综合(1)(2)得x0∈(-∞,-1)∪(4,+∞)
故答案为:(-∞,-1)∪(4,+∞).
点评:此题考查分段函数的性质,要学会分类讨论,此题是一道很基础的题.

练习册系列答案
相关题目
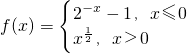 ,若f(x0)>1,则x0的取值范围是________.
,若f(x0)>1,则x0的取值范围是________.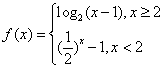 ,若f(x0)>1,则x0的取值范围是
,若f(x0)>1,则x0的取值范围是

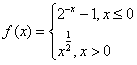 ,若f(x0)>1,则x0的取值范围是
,若f(x0)>1,则x0的取值范围是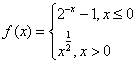 ,若f(x0)>1,则x0的取值范围是
,若f(x0)>1,则x0的取值范围是