题目内容
祖国大陆允许台湾农民到大陆创业以来,在11个省区设立了海峡两岸农业合作试验区和台湾农民创业园,台湾农民在那里申办个体工商户可以享受“绿色通道”的申请、受理、审批一站式服务,某台商在第一年初到大陆创办一座120万元的蔬菜加工厂M,M的价值在使用过程中逐年减少,从第二年到第六年,每年初M的价值比上年初减少10万元;从第七年开始,每年初M的价值为年初的75%.
(1)求第n年初M的价值an的表达式;
(2)设An=
,若An大于80万元,则M继续使用,否则须在第n年初对M更新,证明:必须在第九年初对M更新.
(1)求第n年初M的价值an的表达式;
(2)设An=
| a1+a2+…+an | n |
分析:(1)根据题意,当n≤6时,数列{an}是一个等差数列,当n≥7时,数列{an}中从a6开始的项构成一个等比数列,分别确定它们的首项和公差,公差,写出通项公式,然后进行合并即可.
(2)先对n进行公类,表示出An,利用数列的单调性质确定其最佳项,并与80比较大小,确定n的值.
(2)先对n进行公类,表示出An,利用数列的单调性质确定其最佳项,并与80比较大小,确定n的值.
解答:解:(1)当n≤6时,数列{an}是首项为120,公差为-10的等差数列,
故an=120-10(n-1)=130-10n,
当n≥7时,数列{an}从a6开始的项构成一个以a6=130-60=70为首项,以
为公比的等比数列,
故an=70×(
)n-6,
∴第n年初M的价值an=
.
(2)设Sn表示数列{an}的前n项和,由等差数列和等比数列的求和公式,得:
当1≤n≤6时,Sn=120n-5n(n-1),
An=
=120-5(n-1)=125-5n,
当n≥7时,由于S6=570,
故Sn=570+(a7+a8+…+an)
=570+70×
×4×[1-(
)n-6]
=780-210×(
)n-6,
An=
=
,
∵{an}是递减数列,∴{An}是递减数列,
∵A8=
≈82.734>80,
A9=
≈76.823<80,
所以必须在第九年初对M更新.
故an=120-10(n-1)=130-10n,
当n≥7时,数列{an}从a6开始的项构成一个以a6=130-60=70为首项,以
| 3 |
| 4 |
故an=70×(
| 3 |
| 4 |
∴第n年初M的价值an=
|
(2)设Sn表示数列{an}的前n项和,由等差数列和等比数列的求和公式,得:
当1≤n≤6时,Sn=120n-5n(n-1),
An=
| Sn |
| n |
当n≥7时,由于S6=570,
故Sn=570+(a7+a8+…+an)
=570+70×
| 3 |
| 4 |
| 3 |
| 4 |
=780-210×(
| 3 |
| 4 |
An=
| Sn |
| n |
780-210×(
| ||
| n |
∵{an}是递减数列,∴{An}是递减数列,
∵A8=
780-210×(
| ||
| 8 |
A9=
780-210×(
| ||
| 9 |
所以必须在第九年初对M更新.
点评:本题考查函数模型的建立问题,关键要理解题意,通过相应的数学知识建立数学模型,通过不等式工具、函数最值的思想和方法达到求解的目的.考查转化与化归的思想.

练习册系列答案
相关题目
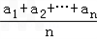 ,若An大于80万元,则M继续使用,否则须在第n年初对M更新,证明:必须在第九年初对M更新.
,若An大于80万元,则M继续使用,否则须在第n年初对M更新,证明:必须在第九年初对M更新.