题目内容
设函数f(x)=(x _ 1)ex _ kx2(k∈R).
(Ⅰ)当k=1时,求函数f(x)的单调区间;
(Ⅱ)当k∈(1/2,1]时,求函数f(x)在[0,k]上的最大值M.
(Ⅰ)当k=1时,求函数f(x)的单调区间;
(Ⅱ)当k∈(1/2,1]时,求函数f(x)在[0,k]上的最大值M.
(Ⅰ)函数 的递减区间为
的递减区间为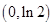 ,递增区间为
,递增区间为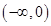 ,
,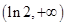 .
.
(Ⅱ)函数 在
在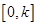 上的最大值
上的最大值 .
.
 的递减区间为
的递减区间为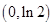 ,递增区间为
,递增区间为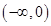 ,
,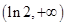 .
. (Ⅱ)函数
 在
在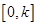 上的最大值
上的最大值 .
.试题分析:(Ⅰ) 当
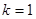 时,
时, 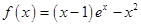 ,
,
令
 ,得
,得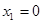 ,
,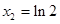
当
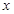 变化时,
变化时,  的变化如下表:
的变化如下表: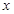 | 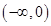 | 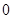 | 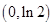 |  | 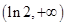 |
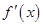 |  | 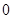 | 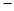 | 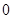 |  |
 | 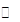 | 极大值 | 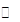 | 极小值 | 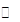 |
 的递减区间为
的递减区间为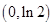 ,递增区间为
,递增区间为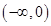 ,
,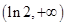 . 6分
. 6分(Ⅱ)
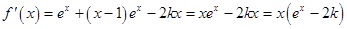 ,
,令
 ,得
,得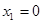 ,
, ,
,令
 ,则
,则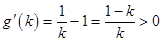 ,所以
,所以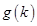 在
在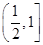 上递增,
上递增,所以
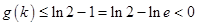 ,从而
,从而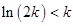 ,所以
,所以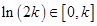
所以当
 时,
时, 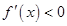 ;当
;当 时,
时, 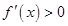 ;
;所以

令
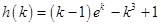 ,则
,则 ,
,令
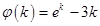 ,则
,则
所以
 在
在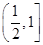 上递减,而
上递减,而
所以存在
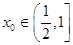 使得
使得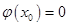 ,且当
,且当 时,
时, 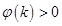 ,
,当
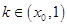 时,
时, 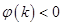 ,
,所以
 在
在 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.因为
 ,
, ,
,所以
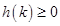 在
在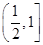 上恒成立,当且仅当
上恒成立,当且仅当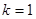 时取得“=”.
时取得“=”.综上,函数
 在
在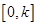 上的最大值
上的最大值 . 14分
. 14分点评:难题,本题较为典型,是导数应用的基本问题。曲线切线的斜率等于在切点处的导函数值。研究函数的最值遵循“求导数,求驻点,研究单调性,确定极值,计算区间端点函数值,比较大小”。本题中函数f(x)在[0,k]上的最大值M.是关于k的函数,处理问题过程中对k存在的讨论易出错。

练习册系列答案
相关题目
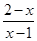 +aln(x-1)(a∈R).
+aln(x-1)(a∈R).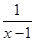 <2ln(x-1)<2x-4(x>2);
<2ln(x-1)<2x-4(x>2);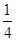 +
+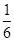 +…+
+…+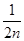 <lnn<1+
<lnn<1+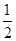 + +
+ +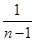 (n∈N*,且n≥2).
(n∈N*,且n≥2).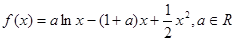
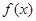 的单调区间;
的单调区间;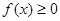 对定义域内的任意
对定义域内的任意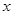 恒成立,求实数
恒成立,求实数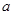 的取值范围.
的取值范围.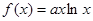 图像上点
图像上点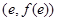 处的切线与直线
处的切线与直线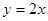 平行(其中
平行(其中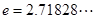 ),
),
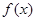 的解析式;
的解析式;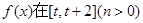 上的最小值;
上的最小值;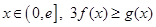 恒成立,求实数
恒成立,求实数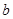 的取值范围。
的取值范围。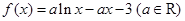
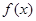 的单调性;
的单调性;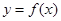 的图象在点
的图象在点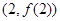 处的切线的倾斜角为
处的切线的倾斜角为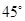 ,对于任意的
,对于任意的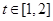 ,函数
,函数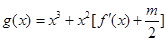 在区间
在区间 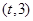 上总不是单调函数,
上总不是单调函数, 的取值范围;
的取值范围;
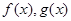 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当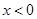 时,
时,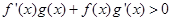 ,且g(-3)=0,则不等式
,且g(-3)=0,则不等式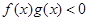 的解集是 ( )
的解集是 ( )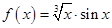 ,则
,则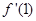 = ( )
= ( )



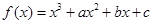 在
在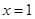 与
与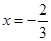 时都取得极值
时都取得极值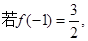 函数f(x)的极值;
函数f(x)的极值;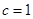 ,方程
,方程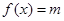 恰好有三个根,求
恰好有三个根,求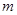 的取值范围.
的取值范围.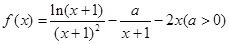 ;
;
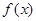 在
在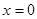 处取极值,求
处取极值,求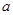 的值;
的值;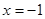 和
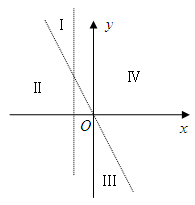
和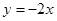 将平面分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域(不包括边界),若
将平面分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域(不包括边界),若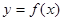 图象恰好位于其中一个区域,试判断其所在区域并求出相应的
图象恰好位于其中一个区域,试判断其所在区域并求出相应的