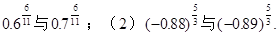题目内容
比较下列各组中两个值大小
(1)0.6
与0.7
(2)(-0.88)
与(-0.89)
.
(1)0.6
| 6 |
| 11 |
| 6 |
| 11 |
(2)(-0.88)
| 5 |
| 3 |
| 5 |
| 3 |
分析:(1)先考察幂函数y=x
,判断指数与0的关系,判断出对应幂函数的单调性,再判断底数的大小,即可得到答案.
(2)先考察幂函数y=x
,判断指数与0的关系,判断出对应幂函数的单调性,再判断底数的大小,结合不等式的性质即可得到答案.
| 6 |
| 11 |
(2)先考察幂函数y=x
| 5 |
| 3 |
解答:解:(1)∵函数y=x
在(0,+∞)上是增函数且0<0.6<0.7<+∞,
∴0.6
<0.7
.
(2)函数y=x
在(0,+∞)上增函数且0<0.88<0.89,
∴0.88
<0.89
,
∴-0.88
>-0.89
,即∴(-0.88)
>(-0.89)
.
| 6 |
| 11 |
∴0.6
| 6 |
| 11 |
| 6 |
| 11 |
(2)函数y=x
| 5 |
| 3 |
∴0.88
| 5 |
| 3 |
| 5 |
| 3 |
∴-0.88
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
点评:本题考查的知识点是幂函数单调性的应用,其中根据指数与0的关系,分析出幂函数的单调性,是解答本题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目