题目内容
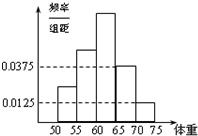 如图是某学校学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数是
如图是某学校学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数是分析:由频率分布直方图可计算出后两组频率之和,因为各小组频率之和为1,可得前三组频率之和,由从左到右的前3个小组的频率之比为1:2:3,计算出第二组的频率,再由第2小组的频数即可得抽取的学生人数.
解答:解:因为各小组频率之和为1,而后两组频率之和为:(0.0375+0.0125)×5=0.25,
所以前三组频率之和为1-0.25=0.75,又因为从左到右的前3个小组的频率之比为1:2:3,
故第二小组频率为:0.75×
=0.25,
因为第2小组的频数为10,则抽取的学生人数是
=40
故答案为:40.
所以前三组频率之和为1-0.25=0.75,又因为从左到右的前3个小组的频率之比为1:2:3,
故第二小组频率为:0.75×
| 2 |
| 1+2+3 |
因为第2小组的频数为10,则抽取的学生人数是
| 10 |
| 0.25 |
故答案为:40.
点评:本题考查频率分布直方图、属基本知识、基本运算的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 个小组的频率之比为
个小组的频率之比为 ,第
,第 小组的频数为
小组的频数为 ,则抽取的学生人数是 .
,则抽取的学生人数是 . 
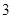 个小组的频
个小组的频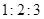 ,第
,第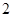 小组的频数为
小组的频数为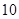 ,则抽取的学生人数是
.
,则抽取的学生人数是
.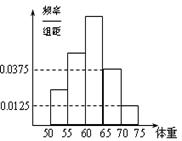
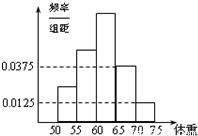 如图是某学校学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数是 .
如图是某学校学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数是 .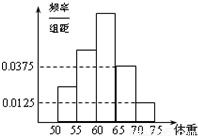 如图是某学校学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数是 .
如图是某学校学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数是 .