题目内容
设圆x2+y2=8内有一点P(-1,2),AB为过点p的直线.
(1)当直线AB的倾斜角为
时,求弦AB的长;
(2)当点p为弦AB的中点时,求直线AB的方程.
(1)当直线AB的倾斜角为
| 3π | 4 |
(2)当点p为弦AB的中点时,求直线AB的方程.
分析:(1)根据题意求出直线AB的斜率,表示出AB的方程,利用点到直线的距离公式求出圆心到直线AB的距离d,再由半径r,利用垂径定理及勾股定理求出弦|AB|的长即可;
(2)根据P为弦AB的中点,得出OP垂直于AB,根据直线OP的斜率求出直线AB的斜率,即可确定出直线AB的方程.
(2)根据P为弦AB的中点,得出OP垂直于AB,根据直线OP的斜率求出直线AB的斜率,即可确定出直线AB的方程.
解答:解:(1)∵kAB=tan
=-1,
∴直线AB的方程为:y-2=-(x+1),即x+y-1=0,
又r=2
,圆心到直线的距离d=
=
,
∴弦|AB|=2
=2
=
;
(2)∵P是AB中点,∴OP⊥AB,
又kOP=-2,∴kAB=
,
则直线AB的方程为y-2=
(x+1),即x-2y+5=0.
| 3π |
| 4 |
∴直线AB的方程为:y-2=-(x+1),即x+y-1=0,
又r=2
| 2 |
| 1 | ||
|
| ||
| 2 |
∴弦|AB|=2
| r2-d2 |
8-
|
| 30 |
(2)∵P是AB中点,∴OP⊥AB,
又kOP=-2,∴kAB=
| 1 |
| 2 |
则直线AB的方程为y-2=
| 1 |
| 2 |
点评:此题考查了直线与圆相交的性质,涉及的知识有:直线的斜率与倾斜角之间的关系,直线的点斜式方程,点到直线的距离公式,垂径定理,以及勾股定理,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
设双曲线
-
=1(a>0,b>0)的离心率为e=
,右焦点为f(c,0),方程ax2-bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| A、在圆x2+y2=8外 |
| B、在圆x2+y2=8上 |
| C、在圆x2+y2=8内 |
| D、不在圆x2+y2=8内 |
 ,求直线AB的斜率;
,求直线AB的斜率;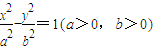 的离心率为
的离心率为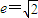 ,右焦点为f(c,0),方程ax2-bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)( )
,右焦点为f(c,0),方程ax2-bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)( )