题目内容
平面上三个力| F1 |
| F2 |
| F3 |
| F1 |
| F2 |
| ||||
| 2 |
| F1 |
| F2 |
(1)
| F3 |
(2)
| F3 |
| F1 |
分析:(1)三个力平衡则三个力的和为
;移项,利用向量模的平方等于向量的平方求出向量的大小.
(2)利用三角函数的余弦定理求出两个向量的夹角大小.
| 0 |
(2)利用三角函数的余弦定理求出两个向量的夹角大小.
解答:解:∵三个力平衡,∴
+
+
=
,(2分)
∴|
|=|
+
|=
=
=
=
+1,(6分)
而
与
的夹角可由余弦定理求得,
cos<
,
>=
=
,
∴
与
的夹角为30°(10分)
则F3与F1的夹角为180°-30°=150°.(12分)
| F1 |
| F2 |
| F3 |
| 0 |
∴|
| F3 |
| F1 |
| F2 |
|
=
12+2×1×
|
4+2
|
| 3 |
而
| F3 |
| F1 |
cos<
| F3 |
| F1 |
12+(
| ||||||||
2×1×(
|
| ||
| 2 |
∴
| F3 |
| F1 |
则F3与F1的夹角为180°-30°=150°.(12分)
点评:本题考查向量模的性质:向量模的平方等于向量的平方、考查三角形的余弦定理.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
平面上三个力F1,F2,F3作用于一点且处于平衡状态,|
|=1N,|
|=
N,
,
的夹角为45°,则
与
的夹角为( )
| F1 |
| F2 |
| ||||
| 2 |
| F1 |
| F2 |
| F3 |
| F1 |
| A、30° | B、150° |
| C、15° | D、135° |
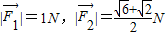 ,
, ,
,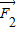 的夹角为45°,则
的夹角为45°,则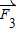 与
与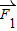 的夹角为( )
的夹角为( )