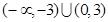题目内容
设f(x)= g(x)是二次函数.若f[g(x)]的值域是[0,+∞),则g(x)的值域是( )
g(x)是二次函数.若f[g(x)]的值域是[0,+∞),则g(x)的值域是( )
(A)(-∞,-1]∪[1,+∞) (B)(-∞,-1]∪[0,+∞)
(C)[0,+∞) (D)[1,+∞)
【答案】
C
【解析】因为g(x)为二次函数,
所以是值域不可能为选项A或B.
若g(x)的值域是[1,+∞),
即|g(x)|≥1,
则f[g(x)]=[g(x)]2≥1,不符合题意.
故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(2004
湖南,12)设f(x)和g(x)分别是定义在R上的奇函数和偶函数,当x<0时,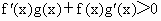 ,且g(-3)=0,则不等式f(x)g(x)<0的解集是
,且g(-3)=0,则不等式f(x)g(x)<0的解集是
[
]|
A .(-3,0)∪(3,+∞) |
B .(-3,0)∪(0,3) |
|
C .(-∞,-3)∪(3,+∞) |
D .(-∞,-3)∪(0,3) |
 ,且g(-3)=0,则不等式f(x)g(x)<0的解集是
,且g(-3)=0,则不等式f(x)g(x)<0的解集是
 ,且g(-3)=0,则不等式f(x)g(x)<0的解集是
,且g(-3)=0,则不等式f(x)g(x)<0的解集是




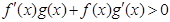 ,且g(-3)=0,则不等式f(x)g(x)<0的解集是
,且g(-3)=0,则不等式f(x)g(x)<0的解集是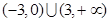 B.
B.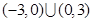
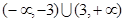 D.
D.