题目内容
(本小题满分12分)
已知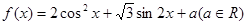
(1)若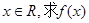 的单调递增区间;
的单调递增区间;
(2)若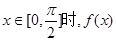 的最大值为4,求a的值;
的最大值为4,求a的值;
已知
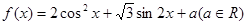
(1)若
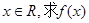 的单调递增区间;
的单调递增区间;(2)若
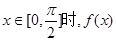 的最大值为4,求a的值;
的最大值为4,求a的值;(1)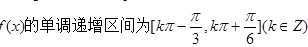
(2)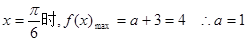 。
。
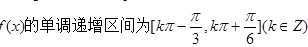
(2)
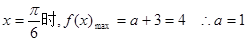 。
。试题分析: (1)要求解函数的单调区间,首先是化简为单一三角函数,然后借助于正弦函数的性质得到结论。
(2)在第一问的基础上,分析得到相位的整体的取值范围,结合三角函数的值域得到最值。
解:(1)
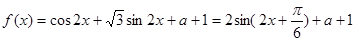 …………4分
…………4分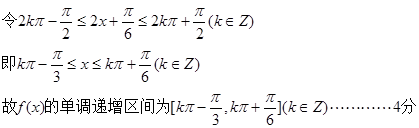
(2)
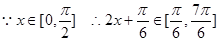
当
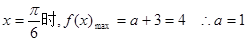 …………12分
…………12分点评:解决该试题的关键是利用二倍角公式,来得到单一三角函数,然后结合三角函数的性质得到单调区间和函数的最值,得到相应的参数a的值。

练习册系列答案
相关题目
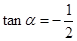 ,则
,则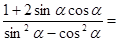 _____ 。
_____ 。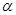 为第二象限角,则
为第二象限角,则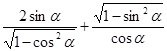 的值是( )
的值是( )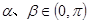 ,且
,且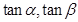 是方程
是方程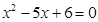 的两根.
的两根.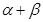 的值. (2)求
的值. (2)求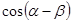 的值.
的值. ,求
,求 的值;
的值; ,求
,求 的值
的值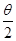 |=-cos
|=-cos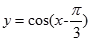 的图象,可将
的图象,可将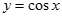 的图象
的图象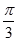 个单位
个单位 ,函数
,函数 在
在 上单调递减,则
上单调递减,则 的取值范围是( )
的取值范围是( )


