题目内容
已知命题p:向量 =(1,1,m)与向量
=(1,1,m)与向量 =(-1,-1,|m|)平行.命题q:方程
=(-1,-1,|m|)平行.命题q:方程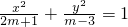 表示双曲线;若“?p”和“p∨q”都为真,求m的取值范围.
表示双曲线;若“?p”和“p∨q”都为真,求m的取值范围.
解:若命题p为真,则m≤0;
若命题q为真,则(2m+1)(m-3)<0,得- <m<3
<m<3
∵“?p”为真∴p假,即m>0 ①
∵“p∨q”,∴q只能为真,即- <m<3 ②
<m<3 ②
由①②得0<m<3
∴所求的范围是(0,3)
分析:先化简两个命题,再由“?p”和“p∨q”都为真,求m的取值范围
点评:本题考查命题的真假判断与应用,正确求解本题,关键是正确理解“?p”和“p∨q”都为真的意义,以及向量平行的条件和二元二次方程表示双曲线的条件.本题题目虽小涉及到的知识点不少,知识性较强,易因为知识掌握得不全面而失分.牢固的双基是做对此类题的保证.
若命题q为真,则(2m+1)(m-3)<0,得-
 <m<3
<m<3∵“?p”为真∴p假,即m>0 ①
∵“p∨q”,∴q只能为真,即-
 <m<3 ②
<m<3 ②由①②得0<m<3
∴所求的范围是(0,3)
分析:先化简两个命题,再由“?p”和“p∨q”都为真,求m的取值范围
点评:本题考查命题的真假判断与应用,正确求解本题,关键是正确理解“?p”和“p∨q”都为真的意义,以及向量平行的条件和二元二次方程表示双曲线的条件.本题题目虽小涉及到的知识点不少,知识性较强,易因为知识掌握得不全面而失分.牢固的双基是做对此类题的保证.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
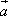 =(1,1,m)与向量
=(1,1,m)与向量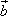 =(-1,-1,|m|)平行.命题q:方程
=(-1,-1,|m|)平行.命题q:方程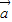 =(1,1,m)与向量
=(1,1,m)与向量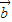 =(-1,-1,|m|)平行.命题q:方程
=(-1,-1,|m|)平行.命题q:方程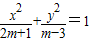 表示双曲线;若“¬p”和“p∨q”都为真,求m的取值范围.
表示双曲线;若“¬p”和“p∨q”都为真,求m的取值范围.