题目内容
已知函数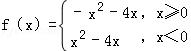
，若f（a﹣2）+f（a）＞0，则实数a的取值范围是（ ）
|
| A． |
| B． | a＞1 | C． |
| D． | a＜1 |
或
或
| ] |
D 【解析】∵x＞0时，﹣x＜0，∴f（﹣x）=x2+4x=﹣f（x）；x＜0时，﹣x＞0，∴f（﹣x）=﹣x2+4x=﹣f（x）， ∴函数f（x）是奇函数 ∵f（a﹣2）+f（a）＞0，∴f（a﹣2）＞f（﹣a）， ∵函数 ∴h（x）=﹣x2﹣4x在[0，+∞）单调递减，h（x）max=h（0）=0 g（x）=x2﹣4x在（﹣∞，0）上单调递减，g（x）min=g（0）=0 由分段函数的性质可知，函数f（x）在R上单调递减 ∵f（a﹣2）＞f（﹣a）， ∴a﹣2＜﹣a，∴a＜1 故选D． |
，若f（a）=2，则a= ．
，若f（a）=2，则a= ．
，若f（a）＞f（-a），求实数a的取值范围．
，若f（a）=-1，则a=（ ）