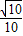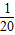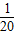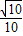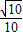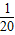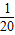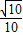题目内容
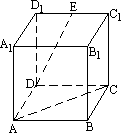
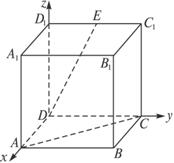
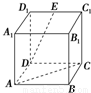
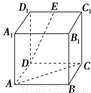
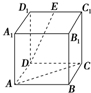 在如图所示的正方体A1B1C1D1ABCD中,E是C1D1的中点,则异面直线DE与AC夹角的余弦值为
在如图所示的正方体A1B1C1D1ABCD中,E是C1D1的中点,则异面直线DE与AC夹角的余弦值为
- A.-

- B.-

- C.

- D.

D
分析:取A1D1中点,连接EF、DF、A1C1,用三角形的中位线和平行线的传递性,证出EF∥AC,得∠DEF(或其补角)就是异面直线DE与AC所成的角.然后在△DEF中求出各边的长,再利用余弦定理即可算出异面直线DE与AC夹角的余弦值.
解答:取A1D1中点,连接EF、DF、A1C1,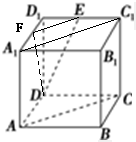
∵正方形ABCD-A1B1C1D1中,A1A∥C1C且A1A=C1C
∴四边形AA1C1C是平行四边形,可得A1C1∥AC
又∵△A1C1D1中,EF是中位线
∴EF∥A1C1,且EF= A1C1.
A1C1.
由此可得EF∥AC,得∠DEF(或其补角)就是异面直线DE与AC所成的角
设正方体的棱长为a,则△DEF中
DF=DE=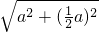 =
= a,EF=
a,EF= A1C1=
A1C1= a
a
由余弦定理,得cos∠DEF=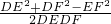 =
= >0
>0
可得∠DEF是锐角,因此∠DEF是异面直线DE与AC所成的角,余弦值为
故选:D
点评:本题在正方体中求异面直线所成角的余弦值,着重考查了正方体的性质和异面直线所成角的定义及求法等知识,属于基础题.
分析:取A1D1中点,连接EF、DF、A1C1,用三角形的中位线和平行线的传递性,证出EF∥AC,得∠DEF(或其补角)就是异面直线DE与AC所成的角.然后在△DEF中求出各边的长,再利用余弦定理即可算出异面直线DE与AC夹角的余弦值.
解答:取A1D1中点,连接EF、DF、A1C1,

∵正方形ABCD-A1B1C1D1中,A1A∥C1C且A1A=C1C
∴四边形AA1C1C是平行四边形,可得A1C1∥AC
又∵△A1C1D1中,EF是中位线
∴EF∥A1C1,且EF=
 A1C1.
A1C1.由此可得EF∥AC,得∠DEF(或其补角)就是异面直线DE与AC所成的角
设正方体的棱长为a,则△DEF中
DF=DE=
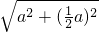 =
= a,EF=
a,EF= A1C1=
A1C1= a
a由余弦定理,得cos∠DEF=
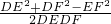 =
= >0
>0可得∠DEF是锐角,因此∠DEF是异面直线DE与AC所成的角,余弦值为

故选:D
点评:本题在正方体中求异面直线所成角的余弦值,着重考查了正方体的性质和异面直线所成角的定义及求法等知识,属于基础题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
 在如图所示的正方体A1B1C1D1ABCD中,E是C1D1的中点,则异面直线DE与AC夹角的余弦值为( )
在如图所示的正方体A1B1C1D1ABCD中,E是C1D1的中点,则异面直线DE与AC夹角的余弦值为( )