题目内容
设某市现有从事第二产业人员100万人,平均每人每年创造产值a万元(a为正常数),现在决定从中分流x万人去加强第三产业.分流后,继续从事第二产业的人员平均每人每年创造产值可增加2x%(O<x<100).而分流出的从事第三产业的人员,平均每人每年可创造产值1.2a万元.
(1)若要保证第二产业的产值不减少,求x的取值范围;
(2)在(1)的条件下,问应分流出多少人,才能使该市第二、三产业的总产值增加最多?
(1)0≤x≤50(2)应分流出50万人才能使该市第二、三产业的总产值增加最多
解析:
(1)由题意,得![]()
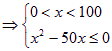
![]() 0≤x≤50
0≤x≤50
(2)设该市第二、三产业的总产值增加f(x) (0<x≤5)万元,则
f(x)=(100-x)(1+2x%)a-100a+1.2ax
=-![]() 。
。
∵x∈(0,50]时,f(x)单调递增,∴x=50时,f(x)max=60a,
即应分流出50万人才能使该市第二、三产业的总产值增加最多

练习册系列答案
相关题目