题目内容
(12分)设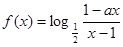 为奇函数,
为奇函数,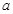 为常数。
为常数。
(1)求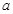 的值;
的值;
(2)证明: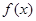 在(1,+∞)内单调递增;
在(1,+∞)内单调递增;
(3)若对于[3,4]上的每一个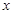 的值,不等式
的值,不等式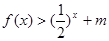 恒成立,求实数
恒成立,求实数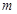 的取值范围。
的取值范围。
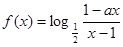 为奇函数,
为奇函数,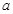 为常数。
为常数。(1)求
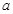 的值;
的值;(2)证明:
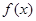 在(1,+∞)内单调递增;
在(1,+∞)内单调递增;(3)若对于[3,4]上的每一个
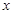 的值,不等式
的值,不等式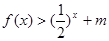 恒成立,求实数
恒成立,求实数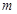 的取值范围。
的取值范围。解:(1)∵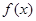 为奇函数,∴
为奇函数,∴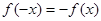 ,
,
∴
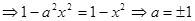
检验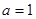 (舍),∴
(舍),∴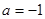
(2)证明:
任取 ,
,
∴
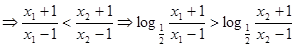
即 ,∴
,∴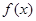 在(1,+∞)内单调递增。
在(1,+∞)内单调递增。
(3)对于[3,4]上的每一个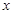 的值,不等式
的值,不等式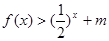 恒成立
恒成立
即 恒成立
恒成立
令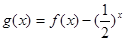 ,只需
,只需
用定义可证 在[3,4]上是增函数,∴
在[3,4]上是增函数,∴
∴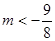 时原式恒成立。
时原式恒成立。
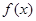 为奇函数,∴
为奇函数,∴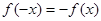 ,
,∴

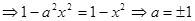
检验
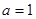 (舍),∴
(舍),∴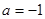
(2)证明:
任取
 ,
,∴

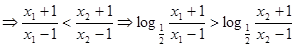
即
 ,∴
,∴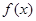 在(1,+∞)内单调递增。
在(1,+∞)内单调递增。(3)对于[3,4]上的每一个
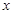 的值,不等式
的值,不等式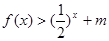 恒成立
恒成立即
 恒成立
恒成立令
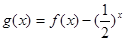 ,只需
,只需
用定义可证
 在[3,4]上是增函数,∴
在[3,4]上是增函数,∴
∴
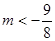 时原式恒成立。
时原式恒成立。略

练习册系列答案
相关题目
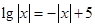 在区间
在区间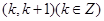 上有解,则满足所有条件的
上有解,则满足所有条件的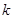 的值的和为
的值的和为 
 在
在 上为减函数,求
上为减函数,求 的取值范围;
的取值范围; 时,求
时,求 的值域;
的值域; 的方程
的方程 在
在 上仅有一解,求实数
上仅有一解,求实数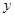 =
=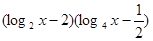 (2≤
(2≤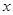 ≤4)
≤4)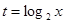 ,求y关于t的函数关系式,t的范围.
,求y关于t的函数关系式,t的范围.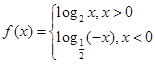 ,若
,若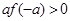 ,则实数
,则实数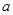 的取值范围是( )
的取值范围是( )
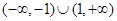


 (1)
(1)

 =
= 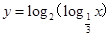 的定义域为 .
的定义域为 . ▲ .
▲ .