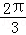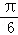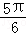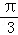题目内容
已知直线y=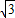 -x与圆x2+y2=2相交于A,B两点,是优弧AB上任意一点,则∠APB=( )
-x与圆x2+y2=2相交于A,B两点,是优弧AB上任意一点,则∠APB=( )A.
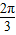
B.
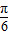
C.
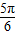
D.
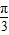
【答案】分析:先求圆心到直线的距离,从而求出AB所对的圆心角,进而求出∠APB.
解答:解:圆心到直线的距离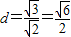 ,
,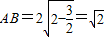 =半径所以AB所对的圆心角是60°,
=半径所以AB所对的圆心角是60°,
所对的圆周角是30°,即∠APB=30°,
选B.
点评:本题主要考查直线与圆相交问题,利用圆心到直线的距离求解时关键.
解答:解:圆心到直线的距离
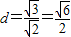 ,
,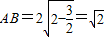 =半径所以AB所对的圆心角是60°,
=半径所以AB所对的圆心角是60°,所对的圆周角是30°,即∠APB=30°,
选B.
点评:本题主要考查直线与圆相交问题,利用圆心到直线的距离求解时关键.

练习册系列答案
相关题目
 -x与圆x2+y2=2相交于A,B两点,是优弧AB上任意一点,则∠APB=
-x与圆x2+y2=2相交于A,B两点,是优弧AB上任意一点,则∠APB=



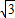 -x与圆x2+y2=2相交于A,B两点,是优弧AB上任意一点,则∠APB=( )
-x与圆x2+y2=2相交于A,B两点,是优弧AB上任意一点,则∠APB=( )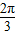
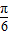
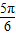
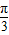
 -x与圆x2+y2=2相交于A,B两点,是优弧AB上任意一点,则∠APB=( )
-x与圆x2+y2=2相交于A,B两点,是优弧AB上任意一点,则∠APB=( )



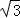 ﹣x与圆x2+y2=2相交于A,B两点,是优弧AB上任意一点,则∠APB=
﹣x与圆x2+y2=2相交于A,B两点,是优弧AB上任意一点,则∠APB=