题目内容
在建立两个变量的回归模型中，分别选择了4个不同的模型，他们的相关指数
如下，其中拟合得最好的模型为
A． 的模型1 | B． 的模型2 |
C． 的模型3 | D． 的模型4 |
B
解析考点：相关系数．
专题：常规题型．
分析：两个变量y与x的回归模型中，它们的相关指数R2，越接近于1，这个模型的拟合效果越好，在所给的四个选项中0.98是相关指数最大的值，得到结果．
解答：解：两个变量y与x的回归模型中，它们的相关指数R2，越接近于1，
这个模型的拟合效果越好，
在所给的四个选项中0.90是相关指数最大的值，
∴拟合效果最好的模型是模型2．
故选B．
点评：本题考查相关指数，这里不用求相关指数，而是根据所给的相关指数判断模型的拟合效果，这种题目解题的关键是理解相关指数越大拟合效果越好．
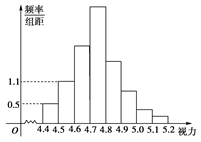
为了了解我校今年准备报考飞行员的学生的体重情况，
将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1︰2︰3，第2小组的频数为12，则抽取的学生人数为
| A．46 | B．48 | C．50 | D．60 |
下列说法错误的是（ ）
| A．自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系； |
| B．线性回归方程对应的直线＝x＋至少经过点其样本数据(x1，y1)，(x2，y2)，…，(xn，yn)中的一个点； |
| C．在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高； |
D．在回归分析中， 为0.98的模型比为0.80的模型拟合的效果好． |
在发生某公共卫生事件期间，有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连 续10天，每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据，一定符合该标志的是( )
| A．甲地：总体均值为3，中位数为4 | B．乙地：总体均值为1，总体方差大于0 |
| C．丙地：中位数为2，众数为3 | D．丁地：总体均值为2，总体方差为3 |
某高中共有
人，其中高一年级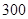
人，高二年级
人，高三年级
人，现采用分层抽样抽取容量为
的样本，那么高一、高二、高三各年级抽取的人数分别为
A． , ,  | B．,, | C．,  , | D．, , |
为了考察两个变量x和y之间的线性相关性，甲、乙两位同学各自独立地做10次和15次试验，并且利用线性回归方法，求得回归直线分别为l1和l2，已知两个人在试验中发现对变量x的观测数据的平均值都是s，对变量y的观测数据的平均值都是t，那么下列说法正确的是 （ ）
| A．l1和l2必定平行 | B．l1和l2有交点（s，t） |
| C．l1与l2必定重合 | D．l1与l2相交，但交点不一定是（s，t） |
甲、乙两名射击运动员在某次测试中各射击20次，两人的测试成绩如下表
| 甲的成绩 | | 乙的成绩 | ||||||||
| 环数 | 7 | 8 | 9 | 10 | | 环数 | 7 | 8 | 9 | 10 |
| 频数 | 6 | 4 | 4 | 6 | | 频数 | 4 | 6 | 6 | 4 |
分别表示甲、乙两名运动员这次测试中成绩的平均数，则有
Ａ．
Ｂ．
Ｃ．
Ｄ．
某文具店出售羽毛球拍和羽毛球，球拍每副定价20元，羽毛球每只定价5元，该店制定了两种优惠方法：①买一副球拍赠送一只羽毛球；②按总价的92%付款。现某人计划购买4副球拍和30只羽毛球，两种方法中，更省钱的一种是 （ ）
| A．不能确定 | B．①②同样省钱 | C．②省钱 | D．①省钱 |
，最大频率为0.32，则
64 
54 
48 
27